МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ
ХІІ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
І кръг
Ученици от 11-12 клас
1задача. Галилей и телескопите. През 1609 г. знаменитият италиански учен Галилео Галилей конструира телескоп и за първи път го използва за наблюдение на небесни светила. През 2009 година се навършват 400 години от това събитие и тя е обявена за Международна година на астрономията.
• Посочете три открития, които е направил Галилей с помощта на своя телескоп.
• Като бъдещи инженери конструктори, вие получавате задача от главния заявител Петър Тодоров да проектирате космически телескоп с такъв диаметър на огледалото, че да се наблюдава достатъчно добре движението на компонентите на затъмнително двойната звезда RZ Cas. За целта разделителна способност на телескопа трябва да е пет пъти по-голяма от необходимата за минимално разделяне на компонентите на звездата. Разстоянието до RZ Cas е 63.5 парсека, а разстоянието между компонентите на звездата е 6.77 слънчеви радиуса. Какъв трябва да бъде диаметърът на главното огледало на телескопа?
Решение:
Изобретяването на телескопа разкрива пред астрономите необикновени възможности за изследване и преобръща много от тогавашните идеи за космоса.
- Благодарение на своите наблюдения с телескоп, Галилео Галилей е открил четирите големи спътници на Юпитер – Йо, Европа, Ганимед и Калисто, които днес наричаме галилееви спътници.
- Той е открил и движението на спътниците около планетата Юпитер. Това е било силен аргумент против господстващата по онова време догматична представа за Земята като център на Вселената, около който единствено се движат всички останали космически тела.
- Галиео пръв е наблюдавал планините и кратерите на Луната. Така станало ясно, че тя е свят, много по-близък до земния, а не е някаква фантастична кристална сфера или пък тяло от т.нар. ефирна материя, нямаща нищо общо със земното вещество, както се е смятало тогава.
- Открил е, че при различни свои положения относно Земята и Слънцето, планетата Венера показва фази, подобно на Луната, а ориентацията на светлата й страна свидетелства за това, че планетата свети с отразена от Слънцето светлина.
- Наблюдавал е слънчевите петна – още едно противоречие с прадставата за идеалната същност на небесните тела. Установил е, че Слънцето се върти около оста си.
- На Галилео Галилей принадлежи и удивителното откритие, че Млечният път се състои от множество отделни звезди.
Означаваме разстоянието до RZ Касиопея с r, а разстоянието между двете компоненти на звездата с r1 . Радиусът на Слънцето е приблизително 700 000 км и следователно 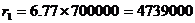 км. км.
Като знаем, че 1 парсек = 3.26 светлинни години, а една светлинна година е разстоянието, което светлината изминава със скорост 300 000 км/сек за една година време, можем да превърнем и r в километри:
r = 63.5 парсека × 3.26 св.г. × 300000 км/с. × 365.25 дни × 24 часа × 3600 сек. ≈ 1.96 × 1015 км
Видимото ъглово разстояние в дъгови секунди между компонентите на двойната звезда ще бъде:


Същото можем да получим и с по-малко пресмятания, ако съобразим, че на разстояние r парсека радиусът на земната орбита, или една астрономическа единица (1 AU) ще се вижда под ъгъл:

Като знаем, че 1 AU = 150 × 106 км, то можем да кажем, че видимото ъглово разстояние между двете компоненти на системата ще е:
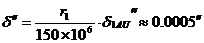
Разделителната способност на телескопа се характеризира с минималното ъглово разстояние между два точкови обекта, при което те могат да се различат като два. Когато става въпрос за наблюдения във видима светлина, това разстояние в дъгови секунди е:
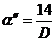
където D е диаметърът на обектива на телескопа, измерван в сантиметри. За да могат да се наблюдават двете звезди, съставящи системата RZ Касиопея, се изисква 5 пъти по-добра разделителна способност от минималната, с която те могат да се различат като две. Следователно условието е:


Оттук за диаметъра на телескопа получаваме:
 см = 1400 м = 1.4 км см = 1400 м = 1.4 км
Критерии за оценяване:
За изброяване на три открития – 3 т.
За разбиране на смисъла на разделителната способност на телескопа и сравнявнението с видимото ъглово отстояние между звездите – 2 т.
За познаване и правилно прилагане на формулите – 3 т.
За верни пресмятания и верен числен резултат – 2 т.
2 задача. Месеци.
• Обяснете какво представляват синодичният месец, драконичният месец и аномалистичният месец. Каква е тяхната продължителност?
• Още преди хиляди години хората забелязали, че 223 синодични месеца, са приблизително равни на 242 драконични месеца и на 239 аномалистични месеца. Проверете това.
• Как се нарича този период от време? Каква е неговата продължителност в години, денонощия и часове? Какво е характерно за този период от време? Имайки предвид какво сте научили за него, пресметнете приблизително колко лунни и слънчеви затъмнения са се случили на Земята от началото на Новата ера досега (т.е. за 2008 години).
Решение:
Синодичният месец е периодът от време между две едноименни лунни фази. Неговата продължителност е
 дни дни
Драконичният месец е периодът между две преминавания на Луната през един и същ възел на своята орбита. Възли са точките, в които лунната орбита около Земята пресича равнината на земната орбита около Слънцето. Продължителността му е 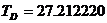 дни. дни.
Аномалистичният месец е периодът между две преминавания на Луната през перигея (или през апогея) на орбитата й около Земята и е с продължителност  дни. дни.
 дни дни
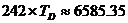 дни дни
 дни дни
Действително получаваме приблизително еднакъв интервал от време. За да намерим продължителността му в години, дни часове, го представяме по следния начин:
 години и 11 дни години и 11 дни
Дробната част от приблизително 0.3 денонощия можем да приравним на около 8 часа. Периодът се нарича сарос и е открит от древните вавилонци преди повече от 2600 години. Това е времето, през което приблизително се повтаря цикълът от слънчеви и лунни затъмнения, настъпващи в определена, доста сложна последователност. Обяснението за тази последователност е, че условията за настъпване на лунно или слънчево затъмнение зависят от фазата на Луната, близостта й до някой от възлите на нейната орбита и моментното й разстояние от Земята.
В един сарос могат да се случат от 69 до 87 затъмнения, но най-често броят на затъмненията е 70 или 71 (от които 43 слънчеви и 28 лунни). Като знаем това, можем да направим приблизителна оценка на броя на затъмненията, които са се случили от началото на Новата ера, т.е. за 2008 години:
 дни дни
 цикъла цикъла
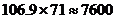 затъмнения затъмнения
Критерии за оценяване:
За първото подусловие – 3 т.
За второто подусловие – 2 т.
За пресмятане на продължителността на периода в години и дни и за посочване на названието му (сарос) – 2 т.
За определението за сароса – 2 т.
За пресмятане на броя на затъмненията – 1 т.
Посочването на исторически подробности за откриването на сароса и обяснението на връзката между различните видове месеци и условията за настъпване на затъмнения не са задължителни и за тях могат да се дават допълнителни точки за награда. В различни източници могат да се намерят леко различаващи се данни за продължителностите на месеците и за броя затъмнения в един сарос (примерно 70, от които 41 слънчеви и 29 лунни и др.). Пресмятания с такива данни да се считат за правилни.
3 задача. Марсианско небе. Северният небесен полюс на Марс е с координати α = 317.7° и δ = 52.9° .
• Коя ярка звезда за марсианците от северното полукълбо на планетата може да играе ролята на Полярна звезда? А за жителите на южното полукълбо?
• В кои съзвездия се намират за Марс точките на равноденствията и слънцестоянията?
Обяснете вашите отговори.
Решение:
Намираме на звездната карта точката с координати
α = 317.7° δ = 52.9°
На повечето звездни карти ректасцензията е в часове и минути, а деклинацията в градуси и дъгови минути, така че може да се наложи да ги превърнем в такива единици:


Точката се намира в съзвездието Лебед и виждаме, че най-ярката звезда в близост до нея е Денеб (α Лебед). Следователно Денеб може да се използва като приблизителен ориентир за посоката север, или полярна звезда в северното полукълбо на Марс. Ако имаше марсианци, те биха учили това в училище.
Южният небесен полюс на Марс е диаметрално противоположна точка от небесната сфера. Нейните координати трябва да бъдат:

или 

Тази точка е в съзвездието Корабни платна. Най-близката по-ярка звезда е δ Корабни платна.
За да намерим точките на слънцестоянията и равноденствията на марсианското небе, вземаме под внимание, че наклонът на марсианската орбита около Слънцето към равнината на земната орбита (еклиптиката) е много малък. Ето защо тези точки трябва да са приблизително на еклиптиката. Намираме на звездната карта северния полюс на еклиптиката. Това е точка с координати  и и 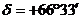 и се намира в съзвездието Дракон. Приблизителното разположение на северния полюс на еклиптиката (П), северния небесен полюс за Земята (PNЗемя) и северния небесен полюс за Марс (PNМарс) е представено на фигурата. и се намира в съзвездието Дракон. Приблизителното разположение на северния полюс на еклиптиката (П), северния небесен полюс за Земята (PNЗемя) и северния небесен полюс за Марс (PNМарс) е представено на фигурата.

Забелязваме, че спрямо сверния еклиптичен полюс PNМарс е на около 90°-100° по посока обратна на часовниковата стрелка от PNЗемя . На фигурата е означена също и посоката към точката на лятно слънцестоене за Земята SSNЗемя , която е с 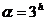 в съзвездието Бик. Оттук следва, че точката на лятно слънцестоене за северното полукълбо на Марс SSNМарс е на около 90° по посока на намаляване на ректасцензията, или западно от SSNЗемя . Тя трябва да е недалеч от пролетната равноденствена точка за северното полукълбо на Земята. Проверката по звездната карта показва, че SSNМарс трябва да е в съзвездието Риби. Тъй като в действителност ъгълът е малко по-голям от 90°, а пролетната равноденствена точка за Земята е западно от центъра на съзвездието Риби, то точката на лятното слънцестоене за Марс би трябвало да е в западния край на Риби, близо до южната им граница с Водолей. Следващите характерни точки за марсианското небе са през 90° една от друга по еклиптиката по посока на нарастване на ректасцензията. Точката на есенното равноденствие за северното полукълбо на Марс ще бъде в съзвездието Бик, на зимното слънцестоене – около границата на съзвездията Лъв и Дева, на пролетното равноденствие – близо до границата между Змиеносец и Стрелец. в съзвездието Бик. Оттук следва, че точката на лятно слънцестоене за северното полукълбо на Марс SSNМарс е на около 90° по посока на намаляване на ректасцензията, или западно от SSNЗемя . Тя трябва да е недалеч от пролетната равноденствена точка за северното полукълбо на Земята. Проверката по звездната карта показва, че SSNМарс трябва да е в съзвездието Риби. Тъй като в действителност ъгълът е малко по-голям от 90°, а пролетната равноденствена точка за Земята е западно от центъра на съзвездието Риби, то точката на лятното слънцестоене за Марс би трябвало да е в западния край на Риби, близо до южната им граница с Водолей. Следващите характерни точки за марсианското небе са през 90° една от друга по еклиптиката по посока на нарастване на ректасцензията. Точката на есенното равноденствие за северното полукълбо на Марс ще бъде в съзвездието Бик, на зимното слънцестоене – около границата на съзвездията Лъв и Дева, на пролетното равноденствие – близо до границата между Змиеносец и Стрелец.
Критерии за оценяване:
За намиране на северния небесен полюс и полярната звезда за Марс – 2 т.
За определяне координатите на южния небесен полюс –2 т.
За намиране на съзвездието, в което е южният полюс и близка ярка звезда – 1 т.
За разбиране на понятията равнодествени точки и точки на слънцестоянията и правилно опериране с тези понятия –2 т.
За правилно определяне положенията им на марсианското небе – 3 т.
4 задача. Земя и Луна.
• Между Земята и Луната има гравитационно привличане. Защо тогава Луната не пада към Земята? А защо Земята не пада към Луната?
Представете си, че Земята и Луната са в междузвездното пространство. Разстоянието между тях е r. Масата на Луната е пренебрежимо малка в сравнение с масата на Земята.
• Ако в първия момент двете тела са неподвижни, какво ще стане по-нататък? Обосновете вашия отговор с алгебрични пресмятания.
• Нека придадем на Луната има начална скорост 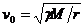 , където М e масата на Земята, а γ е гравитационната константа. Какво ще се случи тогава? Разгледайте различни случаи за посоката на началната скорост на Луната. Пресметнете периодите на движение на Луната около Земята за случаите, в които това е възможно. За останалите случаи приведете само качествени разсъждения. , където М e масата на Земята, а γ е гравитационната константа. Какво ще се случи тогава? Разгледайте различни случаи за посоката на началната скорост на Луната. Пресметнете периодите на движение на Луната около Земята за случаите, в които това е възможно. За останалите случаи приведете само качествени разсъждения.
Решение:
Луната се движи свободно по своята орбита под действие на силата на земно привличане. Всяко такова движение е вид свободно падане. Причината Луната да не пада на Земята (в смисъл да се удари в нея) е, че Луната има достатъчно висока начална скорост, насочена по определен начин.

Нека в даден момент скоростта на Луната е v. За много кратък интервал от време Δt Луната извършва преместване по своята орбита Δr . То може да се разглежда като векторна величина, съставена от две компоненти:
- преместването  , което е равномерно движение по направление на моментната скорост v ; , което е равномерно движение по направление на моментната скорост v ;
- преместването 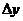 , което е свободно падане към Земята с ускорение, придавано на Луната от гравитационната сила на нашата планета. , което е свободно падане към Земята с ускорение, придавано на Луната от гравитационната сила на нашата планета.
Така че Луната в действителност неперстанно „пада” свободно към Земята. Но тя не може да падне в истинския смисъл на думата към нас, благодарение на притежаваната от нея достатъчно голяма скорост.
С тази скорост Луната се стреми да се движи по инерция и би „избягала” от Земята, ако земното гравитационно въздействие изчезне. Но в резултат от това въздействие траекторията й се изкривява, макар и не дотам, че да падне окончателно на Земята.
Луната също привлича Земята. По същата логика Земята би трябвало да пада към Луната. Причините това да не става, са много подобни на описаните в случая с Луната. Всъщност в системата Земя – Луна Земята не е неподвижна. Луната и Земята се движат около центъра на масите на системата. Така че и Земята има своя орбита и съответно, своя начална скорост относно Луната. Затова тя не пада към Луната, макар че и движението на Земята по орбитата й може да се разглежда като вид свободно падане.
Ако в даден момент Земята и Луната се окажат неподвижни някъде далеч в космоса, те ще започнат да падат свободно по права линия една към друга. Накрая те ще се срещнат в точката, отговаряща на центъра на масите на системата Земя – Луна. За да намерим времето, за което става това, разглеждаме движението на едно от двете тела, например на Луната, в координатна система, в която другото тяло – Земята, е неподвижно. Движението на Луната към Земята представяме като движение по елиптична орбита, толкова силно сплесната, че се е превърнала в отсечка. Голямата полуос на елипсата е r / 2 . Да означим с γ гравитационната константа, а с M и ML – масите на Земята и Луната. Съгласно ІІІ закон на Кеплер:

Търсеното от нас време t от началния момент до срещата на двете тела е равно на половината от орбиталния период Т. Тъй като  , то , то 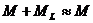 . .

Разбира се, пренебрегнати са и размерите на Земята и Луната.
Скоростта 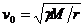 е равна на скоростта, с която Луната би се движила по кръгова орбита с радиус r около Земята. Такава орбита би се осъществила, ако началната скорост е придадена на Луната в посока перпендикулярна на посоката към Земята. Орбиталният период Т0 можем да опрделим от съотношението: е равна на скоростта, с която Луната би се движила по кръгова орбита с радиус r около Земята. Такава орбита би се осъществила, ако началната скорост е придадена на Луната в посока перпендикулярна на посоката към Земята. Орбиталният период Т0 можем да опрделим от съотношението:
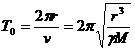
Същия резултат получаваме и ако използваме ІІІ закон на Кеплер:
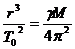
От законите на механиката се извеждат няколко известни следствия, свързани с относителното движение на тяло в гравитационното поле на друго тяло, което ще наричаме гравитационен център. Ако на дадено разстояние от определен гравитационен център едно тяло има начална скорост, която е по-малка от параболичната скорост за това разстояние, то тялото ще се движи по елипса или окръжност около гравитационния център. При различни посоки на началната скорост спрямо направлението към гравитационния център траекториите на тялото ще са елипси с различен ексцентрицитет, но с една и съща голяма полуос. Оттук съгласно ІІІ закон на Кеплер следва, че и орбиталният период на тялото по всяка от тези елиптични траектории ще е един и същ. В нашия случай ако началната скорост на Луната относно Земята е насочена в каквато и да било посока, Луната ще описва около Земята елипса с голяма полуос, равна на r и период, равен на получения от нас период Т0 . В зависимост от размерите на Земята и Луната, при определени посоки на началната скорост Луната ще се сблъска със Земята и тогава няма да има защо да говорим за орбитален период. В частност може началната скорост на Луната да е насочена точно в посока, обратна на посоката към Земята. Тогава можем да разглеждаме траекторията на Луната като елипса с ексцентрицитет 1, която се е изродила в отсечка. Голямата полуос на тази елипса също ще е r и следователно Луната ще се отдалечи на максимално разстояние 2r от центъра на Земята, след което ще започне да пада обратно към нея, докато двете тела се сблъскат. (Тук не разглеждаме факта, че при приближаването на Луната на достатъчно малко разстояние, тя ще бъде разрушена от приливните сили на нашата планета).
Критерии за оценяване:
Това е трудна задача, чието пълно решение по принцип трябва да се оценява с повече от 10 точки. Но на І кръг на олимпиадата тя не бива да има много голяма тежест в сравнение с останалите. Тя е дадена, за да могат да се изявят най-добрите участници. Най-вероятно обясненията и интерпретациите на учениците ще бъдат много различни. Необходимо е да се оценява преди всичко разбирането на физическия смисъл на явленията и закономерностите.
За първото подусловие – 3 т.
За правилен качествен отговор на второто подусловие –2 т.
За алгебрични пресмятания по второто подусловие – 2 т. (Някои могат да пресметнат и къде между Земята и Луната се намира центърът на масите и това също трябва да се оцени).
За пресмятане на орбиталния период в случая на кръгово движение в третото подусловие – 1 т.
За качествените разсъждения по останалите случаи – 2 т.
Дори без да са направени оригинални разсъждения, излизащи извън рамките на официалното решение, при много добре формулирани и задълбочени отговори могат да се дават допълнителни точки за награда.
5 задача. Пасаж. След продължителни опити най-после успешно бе заснет Дядо Коледа! Използвана е била автоматична високоскоростна камера. След първоначалния шок от факта, че елените му са девет, а не осем, както са мислели досега, учените забелязали, че е заснет пасаж на Дядо Коледа по диска на Луната. Оказало се, че най-предната точка на шейната преминала видимия лунен диск за 0.05 секунди.
• Вие разполагате с една от снимките, получени с камерата. Пресметнете от какво разстояние е фотографиран Дядо Коледа.
• С каква минимална скорост се движи в този момент шейната на Дядо Коледа?

Решение:
Дядо Коледа, според сигурни свидетелства, е внушителна фигура и затова приемаме, че е висок 2 метра. Ако мислено го поставим да стои прав в шейната, краката му ще са стъпили на дъното на шейната. Измерваме с линийка и получаваме приблизително 7 мм. Измерваме с линийка и диаметъра на Луната. Получаваме 30 мм. Следователно ъгловият размер на Дядо Коледа е 4.3 пъти по-малък от видимия ъглов размер на Луната. Тъй като ъгловият диаметър на Луната е 30' (30 дъгови минути), то очевидно е, че Дядо Коледа е висок 7' (7 дъгови минути). Нека h е височината на Дядо Коледа, а r е разстоянието от камерата до него. Тогава:
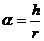 (1) (1)
където α е ъгловият размер на изправената фигура на Дядо Коледа в радиани.
Пресмятяме колко радиана са 7' :
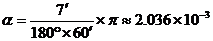 rad rad
От формула (1) пресмятаме разстоянието до шейната:
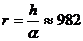 м ≈ 1 км м ≈ 1 км
За  сек. шейната пресича видимия лунен диск. През това време тя изминава разстояние: сек. шейната пресича видимия лунен диск. През това време тя изминава разстояние:
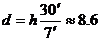 м м
Скоростта на шейната е:
 м/сек. ≈ 620 км/час м/сек. ≈ 620 км/час
Получената скорост е при хипотеза за движение на шейната перпендикулярно на лъча на зрение. Тъй като е възможен някакъв неголям ъгъл спрямо това направление, то полученият резултат е оценка на минималната скорост на движение на шейната на Дядо Коледа.
Критерии за оценяване:
За намиране на информация за ъгловия размер на Луната (или пресмятането му от разстоянието до Луната и диаметъра й) и за предположение за ръста на Дядо Коледа – 3 т.
За пресмятане на разстоянието от фотографа до шейната – 4 т.
За скоростта на шейната – 3 т.
При различни предположания за ръста на Дядо Коледа и намерени данни за Луната резултатите могат да се различават от дадените в решението, но следва да се считат за правилни, ако изчисленията са проведени вярно.
6 задача. Вечерно небе. Наблюдавайте небето рано вечер на югозапад през декември 2008 г. и януари 2009 г.. При ясно време ще виждате две много ярки светила, които приличат на звезди, но са по-ярки от всички звезди.
• Кои са тези космически обекти?
• Защо са толкова ярки?
• С какви имена някога хората в България са наричали по-яркия обект?
• (Незадължително условие). Погледнете тези светила с бинокъл (или телескоп). Какво забелязвате? Направете зарисовки на наблюдаваните обекти. Отбележете датата и часа, а също и с какъв оптически уред сте наблюдавали.
Решение:
Ярките обекти са планетите Венера и Юпитер. Венера е по-яркият обект, а Юпитер – по-слабият.
Венера е най-яркият обект на небето след Слънцето и Луната. Причините за това са три. Първо, Венера е близо до Слънцето. Поради това повърхността й се огрява от по-голямо количество светлина отколкото по-далечните обекти. Второ, Венера е близо до Земята. Това води до повишаване на видимия й блясък поради по-голямото количество светлина, което попада в окото на наблюдателя. Трето, видимата повърхност на Венера е покрита с облаци, които имат висока отражателна способност (албедо). Венера има най-високото албедо в сравнение с останалите планети от Слънчевата система.
Юпитер е ярък през цялата година, защото е най-голямата планета от Слънчевата система, видимата му повърхност има добра отражателна способност, като едновременно с това се намира сравнително далеч от Земята и Слънцето. Затова разстоянието до него не се променя съществено през годината. Сега той върви към съединение със Слъцето, когато ще е най-отдалечен от Земята, но въпреки това е по-ярък от всички звезди на небето.
По-ярката планета – Венера, е била наричана “Вечерница”, “Зорница” или “Деница”, според това дали се е виждала вечер, сутрин или през деня.
Наблюдения.
С бинокъл или малък телескоп могат да бъдат видени дисковете на планетите. При Юпитер могат да се видят две малко по-тъмни ивици, успоредни на екватора, както и четирите най-големи спътници на планетата (галилеевите спътници). Могат да се видят всичките четири спътника или по малко, в зависимост от моментното им положение спрямо планетата. При Венера може да се види единствено фазата на планетата. В момента тя е по-голяма от първа четвърт, като постепенно намалява. Ще бъде в първа четвърт в средата на януари, когато ще е в максимална източна елонгация.
Критерии за оценяване
За правилно посочване кои са обектите – 3 т.
За обяснение на яркостта – 4 т.
За посочване на фолклорните имена на Венера – 3 т.
Дадените в курсив пояснения не са задължителни за оценяване. За наблюдения с бинокъл или телескоп могат да се дават допълни точки за награда.
|