МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА

ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ

ХІІІ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ

  Ученици от 7-8 клас

1 задача. Съставяне на съзвездия.
• Двете животни, които виждате, наистина съществуват в природата. Едно от съзвездията изобразява митично същество, което се състои от части на тези животни. Кое е това съзвездие и от кои части на животните се състои митичното същество?

    • На снимката вляво виждате още     едно истинско животно. Какво трябва     да се добави към неговото тяло, за     да се превърне в митичното     същество, символ на поезията, което     също присъства на небето като     съзвездие?

Решение:

Горните две животни са риба и рядко срещан вид див козел, наречен козирог. От тях може да се състави странното митично същество с глава на козел и опашка на риба. То е изобразено в съзвездието Козирог – едно от зодиакалните съзвездия.

Ако на коня поставим крила, той ще се превърне в митичния Пегас – крилатият кон, символ на летящата поетична мисъл и фантазия. Пегас също присъства на небето като съзвездие.

Козирог

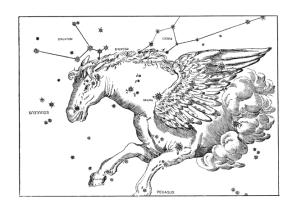
Пегас

Критерии за оценяване:

За всяко подусловие по 4 т., от които за правилно “съставяне” на съзвездието от различните части на животни – 2т., за правилно посочване на името на съзвездието – 2 т.

2 задача. Фантастичен роман. Писател фантаст съчинява поредното си произведение. Ето докъде е стигнал и не знае как да продължи:
“С включването на най-мощните си двигатели звездолетът “Мечта” излезе от околоземна орбита и се понесе към своята далечна цел. Щурманът попита бордовия къмпютър:
І вариант. Приблизително колко път имаме до Орион?
ІІ вариант. Приблизително колко път имаме до Плеядите?”
• Ако вие бяхте бордовият компютър, който разбира малко повече от астрономия, кой вариант бихте посъветвали да избере писателят, за да има научна достоверност, и защо?
• Какво бихте отговорили на щурмана тогава?

Решение:

Съзвездията са възникнали като произволни фигури от звезди, в които с много въображение древните звездобройци са виждали разни легендарни герои и митични същества. Звездите от едно съзвездие могат да бъдат на много различни разстояния от нас. Те могат да са много отдалечени една от друга и по принцип да нямат нищо общо помежду си. Съзвездията не отразяват никакви реални физически връзки, обединяващи звездите. Освен това според съвременното определение съзвездието е област от небето, в която могат да се намират звезди и всякакви други космически обекти като планети, мъглявини и далечни галактики. Следователно въпросът колко път има до съзвездието Орион, е безмислен. Звездолетът не може да пътува до това съзвездие и да пристигне някога там, защото звездите от него не са в някаква обособена и ограничена от всички страни област от пространството.
Звездните купове, като Плеядите, са системи от звезди, които са разположени в ограничена област от пространството, сравнително близо една до друга. Те са реално свързани помежу си от гравитационното привличане и от общия си произход. Ето защо звездолетът наистина може да стигне до Плеядите. Писателят трябва да избере втория вариант.
От нас до Плеядите разстоянието е около 450 светлинни години. Това трябва да отговори бордовият компютър на въпроса на щурмана.

Критерии за оценяване:
За правилно обяснение по вариант І (Орион) – 3 т.
За правилно обяснение по вариант ІІ (Плеядите) – 3 т.
За крайния извод – верен избор на варианта, с който да продължи писателят – 1 т.
За намиране на информация за  разстоянието до Плеядите – 1 т.

3 задача. Компас. Компасът е бил изобретен от древните китайци преди повече от две хиляди години. Вие можете сами да си направите компас. Вземете игла или карфица. Трябва да я намагнитите, като я потриете в силен постоянен магнит. (Ако не можете да намерите магнит в къщи или от приятели, обърнете се за помощ в училищния кабинет по физика или “Човекът и природата”). Забодете иглата в парченце от стиропор или от коркова тапа. Пуснете я да плува в купичка с вода. Вашият компас е готов.

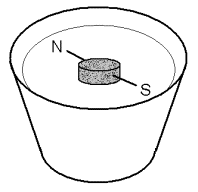
• Определете кой край на иглата показва север и кой юг. За целта наблюдавайте в каква посока е Слънцето около 12 часа на обяд. Тази посока е приблизително юг. Означете посоките север и юг върху парченцето, в което е забодена иглата.
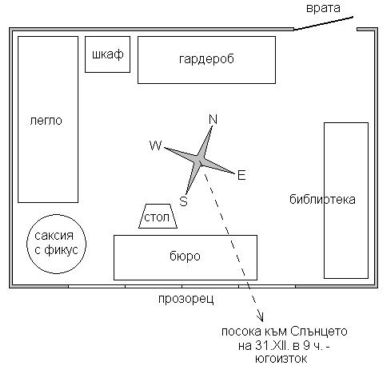
• Нарисувайте приблизителен план на вашата стая. Застанете в средата на стаята и определете с вашия компас посоките север, юг, изток и запад. Означете ги върху плана на стаята.
• Наблюдавайте Слънцето през вашия прозорец. Определете приблизително в каква посока се намира то с помощта на компаса (може да е междинна посока, например югоизток). Означете тази посока върху плана на стаята. Запишете датата и часа, в който сте направили наблюдението.

Важно е при измерванията в непосредствена близост до нашия компас да няма железни предмети, които да отклоняват иглата в неправилна посока. По Слънцето лесно определяме южния полюс на иглата-магнит. Начертаваме план на стаята, определяме посоките на света и ги нанасяме на плана. В даден ден и час наблюдаваме отново Слънцето и определяме посоката към него. Записваме датата и часа.

Критерии за оценяване:
За изработване на компаса и правилно обозначение на северния и южния полюс на намагнитената игла – 2 т.
За плана на стаята, определянето и нанасянето на посоките на света – 4 т.
За наблюдението на Слънцето и определянето на посоката към него – 2 т.

4 задача. Въртене. Когато Земята се върти около оста си, всички ние участваме в това движение – возим се на голяма космическа въртележка.
• С каква скорост се движи точка от екватора на Земята?
• Колко висока кула трябва да построим на екватора, така че върхът й да се движи със скорост, която е с 1 м/с по-голяма от скоростта на земната повърхност?

Екваториалният радиус на Земята е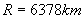. Обиколката на Земята по екватора е:

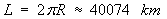
Скоростта на точка от екватора ще бъде:

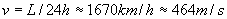
Пътят, изминат от точка на върха на кулата при едно завъртане на Земята, ще бъде:

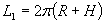
където  H  е височината на кулата. Скоростта на тази точка ще бъде:

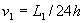
Трябва да бъде изпълнено условието:

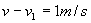
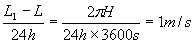
Оттук следва:

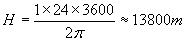
Необходимата близо 14-километрова височина на кулата съществено надвишава най-високия планински връх на Земята Еверест. Тя ни показва още веднъж огромния мащаб на размерите на Земята в сравнение с нашите човешки мерки.
Уточнение: За получаването на скоростта на движение на точка от земната повърхност по принцип трябва да се използва продължителността на звездното денонощие – 23h56m, а не слънчевото денонощие от 24h. Но в задачата се иска само приблизителна оценка, така че грешката от използването на продължителността на слънчевото денонощие не е съществена.

Критерии за оценяване:
За първото подусловие общо 3т., от които за намиране на информация за радиуса на Земята и правилна математическа постановка – 2 т. и за верен числен отговор – 1 т. (Забележка: Някои ученици навярно ще намерят информация направо за обиколката на Земята по екватора. В такива случаи решението да се оценява също като правилно).
За второто подусловие общо 5 т., от които за правилна математическа постановка 4 т. и за верен числен отговор 1 т.

5 задача. Необикновена снимка. Разгледайте  снимката на Земята, направена от орбиталната станция “Мир” на 11 август 1999 г., по време на едно забележително астрономическо явление.

• Какво представлява тъмното петно, което се вижда върху Земята?
• Какво явление бихте наблюдавали, ако се намирахте на земната повръхност в централната част на тъмното петно?
• Какво бихте виждали, ако се намирахте в размитата периферия на тъмното петно?

Решение:

На снимката се вижда част от дневната страна на нашата планета, осветена от Слънцето. Тъмното петно е сянката на Луната върху Земята. Ако се намираме на Земята в централната част на тъмното петно, ще виждаме как Луната напълно закрива Слънцето – ще наблюдаваме пълно слънчево затъмнение. Размитата периферия на тъмното петно е зоната на полусянката на Луната. Ако се намираме там, ще виждаме Слънцето частично закрито от Луната – ще наблюдаваме частично слънчево затъмнение.

Критерии за оценяване:
За верен отговор на първото подусловие – 2 т.
За второто и третото подусловие  по 3 т, от които 1.5 т. за верен отговор и 1.5 т. за обяснение.

6 задача. Древна астрономия.

Тази рисунка е издялана върху камък преди много хиляди години. На нея първобитният човек търпеливо и последователно, ден след ден е отразявал нещо, което е наблюдавал на небето. Фигурките са направени неточно и непохватно, времето също е повлияло върху тях. Но те изобразяват повтаращи се явления, които можем да разпознаем и днес. Какво представлява рисунката? Обосновете подробно вашето предположение.

Решение:

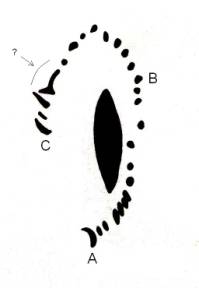На камъка са изобразени лунните фази за всеки ден в рамките на един синодичен месец.    Ако   предположим,   че авторът  на  рисунката  е обитавал северното полукълбо, то сърпът, обърнат с изпъкналата си страна надясно и означен с А, съответства на младата Луна – фаза около един ден след новолуние. В следвашите дни астрономът от първобитната епоха е отразявал ежедневно промяната на вида на Луната, докато се стигне до пълнолунието, означено с В на рисунката. Накрая старата Луна, означена с С, е  изглеждала като тънък сърп, обърнат с изпъкналата си страна наляво. В следващите 1-2 дни Луната не се е виждала, което съответства на празното място между С и А, и после започва новият цикъл на лунните фази.

Лунните фази се сменят с период един синодичен месец, който се равнява приблизително на 29.5 денонощия. Не е съвсем ясно колко последователни лунни фази са отбелязани на камъка. Бихме могли да приемем, че означеното със стрелка изображение представлява всъщност две изображения, които изглеждат слети поради някаква пукнатина или друга случайна следа върху камъка. Тогава можем да считаме, че на камъка са отбелязани 27 последователни лунни фази. Липсващите още две съответстват на интервала от време около новолунието, когато Луната не се наблюдава.

Критерии за оценяване:
За правилен отговор на въпроса – 2 т.
За правилно посочване на последователността на смяната на фазите и техните названия – 3 т.
За разсъждения относно броя на лунните изображения и дните в синодичния месец – 3 т.