МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ
Х НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
http://astro-olymp.org
ІІ кръг - задачи и решения
Ученици от 11-12 клас
1 задача. Измерената лъчева скорост на звезда с ректасцензия 6 h е 65 км/сек, а половин година по-късно лъчевата й скорост е 95 км/сек. Каква е деклинацията на звездата? Лъчевата скорост на една звезда е равна на компонентата от относителната скорост на звездата спрямо Земята, която е насочена по направление на зрителния лъч от земния наблюдател към звездата.
Решение: Промяната на наблюдаваната лъчева скорост на звездата по отношение на Земята се дължи на орбиталното движение на Земята около Слънцето. Скоростта, с която Земята обикаля около Слънцето, можем да пресметнем, като знаем разстоянието r от Земята до Слънцето и орбиталния период на нашата планета Т = 1 година:
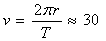 км/сек. км/сек.

Да предположим, че звездата лежи в равнината на земната орбита около Слънцето. Максималните отклонения на относителната лъчева скорост на звездата спрямо Земята от средната й стойност за една година ще се получават в точките 1 и 2. Разликата между измеренита стойности на лъчевата скорост на звездата в тези две точки ще бъде 2v=60 км/сек. При зведата, разглеждана в задачата лъчевите скорости са измерени през интервал от време половин година, т.е. те се отнасят също за две диаметрално противоположни точки от земната орбита. Но разликата между тях е само:
95 км/сек – 65 км/сек = 30 км/сек.
Ако звездата лежи в равнината на земната орбита около Слънцето, това би означавало, че измерванията не са направени в точките 1 и 2, а в други две подходящо разположени противоположни точки. От условието на задачата обаче става ясно, че е реализирана другата възможност – звездата да не лежи в равнината на земната орбита или еклиптиката. Ще пресметнем максималното ъглово отстояние на звездата от орбиталната равнина на Земята (еклиптиката) – нейната еклиптична ширина β . При него, за да се получи дадената разлика между лъчевите скорости на звездата, измерванията трябва да са направени в точките 1' и 2' от земната орбита.
Тогава в случая, когато Земята е в точка 2' , поради движението на Земята около Слънцето, към относителната лъчева скорост на звездата спрямо нас се добавя 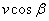 . Това е проекцията на относителната скорост на звездата, дължаща се на земното движение, върху зрителния лъч към нас. . Това е проекцията на относителната скорост на звездата, дължаща се на земното движение, върху зрителния лъч към нас.
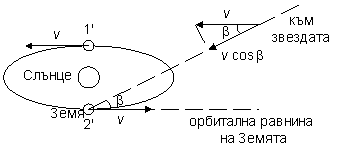
Съответно, когато Земята е в точка 2' , същата стойност ще трябва да се извади от лъчевата скоростна звездата. Така разликата между относителните лъчеви скорости на звездата спрямо нас в моментите, когато нашата планета е в точките 1' и 2' ще бъде 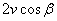 . Така можем да пресметнем β от следното съотношение: . Така можем да пресметнем β от следното съотношение:
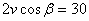 км/сек. км/сек.
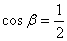
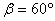
Следователно, еклиптичната ширина на звездата може да е от 0° до ± 60° . В условието е казано, че ректасцензията на звездата е 6 h . Това е ректасцензията на точката на лятно слънцестоене. Тази точка, лежаща на еклиптиката, отстои от небесния екватор на +23.5° . Това е нейната деклинация. Оттук следва, че деклинацията на звездата е + 83.5° или –36.5° .
При хипотеза, че измерените лъчеви скорости не са съответно минималната и максималната лъчева скорост на звездата, т.е. Земята не е в точките 1' и 2', в момента на наблюденията, то деклинацията може да бъде между 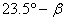 и и 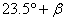 , т.е. от –36.5° до + 83.5° . , т.е. от –36.5° до + 83.5° .
2 задача.
На фигурата са дадени еволюционни трекове, описващи началните стадии от живота на звезди с различни маси (дадени в единици М - масата на Слънцето). Това са линии, които описват изменението на параметрите на все още формиращите се звезди, преди те да се установят на главната последователност. Разгледайте трека на звездата с маса 9 М в участъка между точките А и В и опишете:
• Как се променят температурата и светимостта на звездата в този участък.
• Как се променя радиусът на звездата? Дайте приблизителна количествена оценка за отношението на радиуса на звездата в момента, когато е била в точка А към радиуса й, когато е достигнала до точка В.
• Какво става със звездата? 
Решение:
От графиката се вижда, че температурата на формиращата се звезда в точка А от нейния еволюционен трек е ТА ≈ 5000 К, а в точка В е ТB ≈ 20 000 К. Температурата на звездата, която е по-правилно да наричаме все още протозвезда, се повишава. Същевременно светимостта й L почти не се променя. За да запазва протозвездата една и съща мощност на излъчване при повишаваща се температура, тя трябва да намалява своя радиус. За параметрите на протозвездата в моментите, когато състоянието й се е описвало с точките А и В от еволюционния трек, можем да напишем:
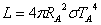
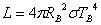
където RА и RB са стойностите на радиуса на звездата в точките А и В, а σ е константата на Стефан-Болцман. Като разделим почленно двете равенства, получаваме:
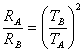
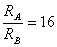
Радиусът на протозвездата намалява 16 пъти. Участъкът АВ от еволюционния трек на протозвездата отразява един период от нейното свиване под действие на собствената й гравитация. Освободената при това енергия води до повишаване на температурата на протозвездата.
3 задача.
• Защо пълната фаза на лунно затъмнение може да трае повече от час, а пълната фаза на слънчево затъмнение – само няколко минути?
• Лунно затъмнение можем да наблюдаваме по различно време на нощта. А можем ли да видим лунно затъмнение през деня? Обяснете своя отговор. Решение: Лунно затъмнение се получава, когато Луната попадне в сянката на Земята.
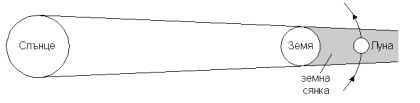
На разстоянието от Земята до Луната земната сянка е около два и половина пъти по-голяма по диаметър от самата Луна. На Луната е необходимо значително време, за да премине през земната сянка. Затова пълната фаза на лунното затъмнение е продължителна.
Слънчево затъмнение се получава, когато лунната сянка попадне върху Земята.
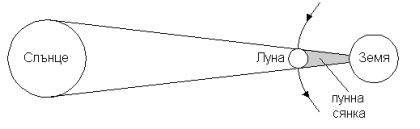
Лунната сянка е с диаметър около 200 км. Движението й по земната повърхност се определя от движението на Луната по нейната орбита около Земята и въртенето на Земята около нейната ос. Необходимо е много малко време, за да премине цялата лунна сянка през даден наблюдателен пункт на Земята. Затова пълната фаза на слънчевото затъмнение е много кратка.
Да си представим наблюдател в точка Х на Земята. За него линията АВ е математическият хоризонт. 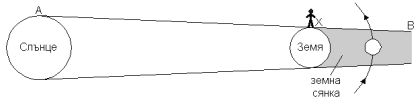
Тази линия е на границата между областта от земната повърхност, където Слънцето е изцяло под хоризонта, и областта от земната повърхност, където поне част от Слънцето е над хоризонта. Условно казано, точката Х е на границата между деня и нощта. Същевременно линията АВ е на границата на земната сянка. Вижда се, че както Слънцето, така и земната сянка, в която трябва да е Луната при затъмнение, за наблюдателя Х са под хоризонта. Следователно няма точка на Земята, от която едновременно в някакъв момент да виждаме и Слънцето, и Луната по време на затъмнение, т.е. да виждаме лунно затъмнение през деня. Това, обаче, е теоретично твърдение. Поради рефракцията, например, ние виждаме небесните обекти на по-голяма височина над хоризонта от действителната. На самия хоризонт рефракцията е над 0.5° . Видимите ъглови диаметри на Слънцето и Луната са по 0.5° , следователно рефракцията може да доведе до това, че да е възможно едновременното наблюдение и на Слънцето, и на Луната когато е близо до пълнолуние, над хоризонта, включително и тогава, когато има лунно затъмнение. Можем да увеличим още повече тази възможност, ако се качим на планински връх, така че физическият хоризонт за нас да бъде под математическия хоризонт. 4 задача. Участничка в астрономическата олимпиада си мечтае да бъде като Пипи Дългото чорапче и да може да вдигне кон. Е, ако не на Земята, то поне на Луната. Конят тежи 240 килограма.
• Пресметнете колко би тежал конят на Луната. Как мислите, ще можете ли вие наистина да го повдигнете там?
• Пипи е решила да ви докаже, че и на Земята може да намали теглото на коня. С каква скорост трябва да тича тя по земния екватор, за да бъде носеният от нея кон толкова лек, колкото би било теглото му на Луната?

Решение:
Нека означим с М и М1 съответно масите на Земята и Луната, с R и R1 – техните радиуси, а с g - гравитационната константа. Означаваме също така с g и g1 ускоренията на силата на тежестта съответно на земната и на лунната повърхност. Тогава можем да напишем:
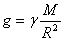 (1) (1)

Разделяме почленно двете равенства и получаваме:
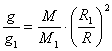
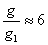
Следователно на лунната повърхност теглото на коня ще е 6 пъти по-малко, отколкото на Земята. На Луната конят ще тежи 240 / 6 = 40 кг. Дали бихме могли да повдигнем коня на Луната зависи от нашите сили. Можем да допуснем, че една участничка в олимпиадата е в състояние да поне да повдигне товар от 40 кг, ако се намира на Земята. Тогава тя ще може да повдигне коня на Луната. Затруднения биха й създали нейният скафандър и разбира се, скафандърът на коня. Но тези затруднения могат да се елиминират, ако си представим, че момичето и конят се намират в изолирана лунна база, където има въздух за дишане. По-сериозна пречка би се оказало това, че момичето трудно ще намери начин да обхване с ръцете си коня, за да го повдигне.
За да стане конят, носен от Пипи, по-лек на Земята, Пипи трябва да тича по земния екватор в посоката на въртене на Земята. Така “олекването” на коня ще се дължи на центробежната сила, която ще му действа. Центробежната сила ще се определя от скоростта на движение на коня около оста на Земята. Тази скорост е:
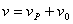 (2) (2)
където vP е скоростта, с която бяга Пипи, а vP е линейната скорост на движение на точка от екватора при въртенето на Земята около оста й.
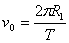
където 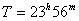 е периодът на околоосно въртене на Земята. е периодът на околоосно въртене на Земята.
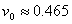 км/сек. км/сек.
Центробежната сила, действаща върху коня, ще му придава ускорение:
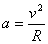 (3) (3)
което е насочено нагоре – противоположно на земното ускорение g . За да олекне конят 6 пъти в резултат от това, и да се чувства като на Луната, трябва да е изпълнено следното съотношение:
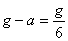
Или:
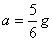
Тогава от (3) получаваме:
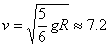 км/сек. км/сек.
Като имаме предвид (2), можем да пресметнем скоростта на Пипи Дългото чорапче:
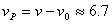 км/сек км/сек
Това е внушителна скорост, сравнима с първа космическа скорост, но нека не забравяме, че Пипи е най-силното момиче на света...

Рисунка - Диана Нанева, VІІ клас, гр. Варна
5 задача. 
" . . . Но на твоята толкова малка планета стигало ти е само да дръпнеш стола си на няколко крачки. И всеки път, когато ти се е поисквало, ти си гледал вечерната дрезгавина . . .
- Един ден видях слънцето да залязва четиридесет и четири пъти!
И малко след това ти добави:
- Знаеш ли. . . когато човек е много тъжен, обича слънчевите залези . . . "
Ако астероидът на Малкия принц се завърта около оста си за 24 часа и той е видял четиридесет и четирите залеза за 3 часа, то на какво разстояние от Слънцето се е намирала тогава неговата планета?
Коя от планетите Малкият принц ще вижда по-ярка от своя астероид –
Земята или Венера? Колко пъти видимият за него блясък на едната планета
ще се отличава от блясъка на другата? Считайте, че всяка от планетите е в
положение, при което има максимален блясък. Диаметрите на двете планети са приблизително еднакви, а албедото (отражателната способност) на Венера е два пъти по-голямо от това на Земята. Решение: За да направим пресмятанията, приемаме че Малкият принц наблюдава залезите от екватора на своя астероид. Нека залезът на Слънцето започва, когато най-долната точка на видимия слънчев диск докосне хоризонта, и завършва, когато Слънцето изцяло се скрие под хоризонта. Това означава, че за интервала от време, докато трае залезът, Слънцето изминава един свой видим ъглов диаметър при видимото си денонощно движение по небесната сфера. Астероидът на Малкия принц се завърта около оста си за 24 часа. Следователно за три часа Слънцето ще измине ъглово разстояние, равно на 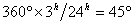 . През тези три часа Малкият принц е видял 44 слънчеви залеза, което означава, че Слънцето се е преместило на 44 свои ъглови диаметъра по небето. Следователно видимият от астероида ъглов диаметър на Слънцето е . През тези три часа Малкият принц е видял 44 слънчеви залеза, което означава, че Слънцето се е преместило на 44 свои ъглови диаметъра по небето. Следователно видимият от астероида ъглов диаметър на Слънцето е 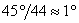 . Видимият от Земята ъглов диаметър на Слънцето е: . Видимият от Земята ъглов диаметър на Слънцето е:
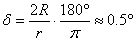
където R е радиусът на Слънцето, а r е разстояниеот от Земята до Слънцето. Оттук следва, че астероидът на Малкия принц се намира приблизително на двойно по-близко разстояние до Слънцето, отколкото нашата планета, или на 150 000 000 / 2 = 75 000 000 км..
Осветеността Е , която Слънцето създава върху Земята, е обратно пропорционална на квадрата на разстоянието r от Земята до Слънцето:
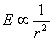
Видимият блясък на Земята за Малкия принц от неговия астероид се определя от осветеността, която Земята създава върху него. За нея можем да напишем:
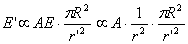
където А е албедото на Земята, R е радиусът й, а 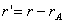 е разстоянието от Земята до астероида , когато Земята е в опозиция на астероида ,най-близо е до него и би била най-ярка. е разстоянието от Земята до астероида , когато Земята е в опозиция на астероида ,най-близо е до него и би била най-ярка.
От справочните данни виждаме, че Венера е по-отдалечена от Слънцето, отколкото астероида на Малкия принц и се явява за него също външна планета, както и Земята. Аналогично за осветеността, която Венера създава върху астероида на Малкия принц, можем да напишем:
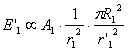
където с индекс 1 сме означили съответните величини за Венера. Очевидно, тъй като Венера е по-близо както до Слънцето, така и до астероида, има почти същия радиус като Земята и двойно по-високо албедо, тя трябва да е с по-силен видим блясък за Малкия принц, отколкото Земята. Като имаме предвид, че 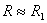 и и 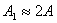 , за отношението на видимия блясък на Венера към този на Земята получаваме: , за отношението на видимия блясък на Венера към този на Земята получаваме:
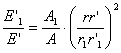
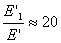
При наблюдение от астероида на Земята и на Венера в опозиция, Венера ще е около 20 пъти по-ярка от Земята.
Справочни данни :
Радиус на Земята – 6378 км
Радиус на Луната – 1738 км
Маса на Земята – 5.98×1024 кг
Маса на Луната – 0.735×1023 кг
Гравитационна константа – 6.67×10-11 м3 / кг.сек2
Разстояние от Земята до Слънцето – 150×106 км
Разстояние от Земята до Слънцето – 108×106 км
Радиус на Слънцето 700 000 км |