|
МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ
ХІІ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
ІІ кръг
Ученици от 9-10 клас
1 задача. Звезди. Както знаем, поради видимото денонощно въртене на небесната сфера, звездите променят своето положение спрямо хоризонта и посоките на света. Има звезди, които изгряват и залязват, има звезди, които са незалязващи и такива, които са неизгряващи. Дали има места по земната повърхност, откъдето едни и същи звезди в горна и долна кулминация са на еднакво ъглово отстояние от хоризоната? Къде са тези места? Какви звезди биха отговаряли на тези условия? Има ли такива звезди?
При решаването на задачата не отчитайте рефракцията.
Решение:
Нека пренебрегнем собственото движение на звездите.
Кулминация на звезда е преминаването й през меридиана на мястото. Кулминацията, при която звездата е на по-голяма височина над хоризонта, наричаме „горна“, другата кулминация наричаме „долна“. Долната кулминация може да се случи и под хоризонта на наблюдателя.
Да разгледаме двата характерни случая – звезда гледана от екватора и от полюса, и общия случай – звезда гледана от място с междинна географска ширина.
На екватора всички звезди са изгряващи и залязващи. Ако не отчитаме рефракцията, полюсите лежат на хоризонта а звездите се движат по малки кръгове, които са наполовина над хоризонта и нополовина – под него. Очевидно е, че в горна и долна кулминация звездите ше бъдат на едно и също ъглово разстояние от хоризонта h = 90 - d, където d е деклинацията на звездата. Ако звездата е на небесния екватор, то в горна кулминация тя ще преминава през зенита, а в долна – през надира. Ако звездата е на някой от небесните полюси, то тя и в горна и в долна кулминация ще се намира на хоризонта. Следователно, когато сме на екватора на Земята, всички звезди ще са на едно и също ъглово разстояние от хоризонта в горна и долна кулминация.
На полюсите на Земята звездите се движат успоредно на хоризонта. Тук не може да се дефинира понятието меридиан на мястото и следователно не може да се определи момент на кулминация на звездите. Бихме могли да кажем, че за полюсите въпросът е безсмислен. Но, при голямо желание, бихме могли и да приемем, че всички звезди по всяко време са и в горна и в долна кулминация (т.е. всеки меридиан е меридиан на мястото) и условието е изпълнено за всички звезди, при това във всеки един момент от време.
Ако не сме на екватора или полюса има само един денонощен паралел, за който се изпълнява исканото условие. Този паралел съвпада с небесния екватор. Само ако звездата се намира на небесния екватор, тя ще е на едно и също ъглово разстояние от хоризонта в горна и долна кулминация. В горна кулминация звездата ще е над хоризонта, а в долна – под хоризонта. Разбира се, ако звездата е точно в небесния полюс, горната и долна кулминации съвпадат и условието е изпълнено.
Съществуват ли звезди, които изпълняват поставените условия?
За първия случай, когато сме на екватора, това са всички звезди на небето.
За случая на полюса, както видяхме, има две възможности – или няма нито една звезда, ако приемем, че необходимите понятия не могат да бъдат дефинирани, или, във втория случай, това отново са всички звезди на небето.
За случая на междинна географска ширина въпросът е много по-сложен.
Нека приемем, че звездите са точкови обекти, т.е. ъгловите им размери са нула. За да е изпълнено условието за равенство на ъглите звездата трябва да е на небесния екватор. При това трябва да е съвсем точно на небесния екватор. Тъй като звездите са точки, разположени в значителна степен случайно по повърхнина, макар и въображаема (небесната сфера), то вероятността някоя звезда да попадне на точно определена линия (небесния екватор) е практически нула. Ако, обаче, приемем че звездите имат крайни, макар и малки, ъглови размери и приемем, че една звезда е на екватора когато той пресича нейния диск, то тогава вероятността да има звезди на екватора е различна от нула, дори и да е много малка.
Същото се отнасят и за случая на звезда точно на небесния полюс.
Всички досегашни разсъждения са направени при едно съществено приближение. Ние негласно приехме, че оста на Земята е неподвижна, т.е. че тя не променя своята ориентация в пространството. Това, обаче, не е така. Поради гравитационното влияние на Луната и Слънцето и поради това, че формата на Земята не е идеално сферична, земната ос прецесира с период около 26000 години, като описва в пространството конус (в първо приближение) с ъгъл при върха 47° и ос насочена към полюса на еклиптиката. Прецесията води до непрекъсната промяна на ориентацията в пространството на небесната ос, на небесния екватор и следователно на моментните координати на звездите и в частност на деклинацията. Дали прецесията премахва всяка възможност условието да бъде изпълнено? Това не е съвсем така. В близост до големия кръг, който минава през еклиптичните полюси и равноденствените точки, деклинацията практически не се променя вследствие на прецесията. В определени моменти от време звезди ще попадат на място, до този голям кръг, в което тяхната деклинация в една горна кулминация ще е точно равна на деклинацията им в следваща долна кулминация. Това ще е вярно само за съответната звезда в точно определен момент от време и следователно за точно определена географска дължина на земната повърхност. Това ще е вярно за съответната точка от екватора както и за полюса. За междинни географски ширини условието ще се изпълни само ако звездата, и в двата момента от време, се намира на небесния екватор. Ако отчетем и прецесията на еклиптиката, т.е. отчетем това, че „окръжността“, която северният небесен полюс описва по небесната сфера, не е затворена, а е по-скоро спирала, то разсъжденията ни от предходния абзац пак ще са верни. Единствено ще се промени, много малко, положението на звездата до разглеждания голям кръг, минаващ през точките на слънцестоене. Двете положения, отговарящи на кулминациите на звездата, вече няма да са симетрично разположени относно големия кръг (за централен момент от време), а ще са леко преместени в една от посоките така, че да се компенсира промяната на деклинацията вследствие на прецесията на еклиптиката.
2 задача. RZ Cassiopeiae. Затъмнително двойната звезда RZ Cassiopeiae представлява система, която се състои от две звезди, обикалящи около общия си център на масите. Орбиталната им равнина е разположена спрямо нас така, че звездите периодично се закриват една друга. Затова в кривата на блясъка на RZ Cas има редуващи се главни и вторични минимуми.
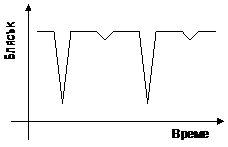
Следващата таблица съдържа данни за двете компоненти на системата RZ Cas.
Компоненти |
А |
В |
Температура |
8 600 K |
4 700 K |
Радиус |
1.67 слънчеви радиуси |
1.94 слънчеви радиуси |
• Колко пъти видимият блясък на затъмнително двойната звезда в момент на главен минимум (когато по-слабата компонента закрива по-ярката) е по-слаб, отколкото в максимум?
• Пресметнете амплитудата на изменение на звездната величина на променливата звезда.
Считайте, че затъмнението на едната компонента от другата е централно.
Решение:
От данните можем да изчислим светимостите на двете компоненти:
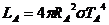 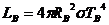
където ТА и ТВ са температурите на двете компоненти, RA и RB са техните радиуси, а σ е константата на Стефан-Болцман. Данните показват, че по-слабата компонента е В. Когато блясъкът на променливата звезда е максимален, ние виждаме светлина и от двете компоненти – те не се закриват една друга. Следователно осветеността Emax , създадена от двойната звезда тогава, е пропорционална на 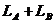 . При главен минимум получаваме светлина само от по-слабата компонента В и осветеността Emin , създавана в такъв случай е пропорционална на LB . По-нататък пресмятаме: . При главен минимум получаваме светлина само от по-слабата компонента В и осветеността Emin , създавана в такъв случай е пропорционална на LB . По-нататък пресмятаме:
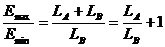
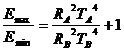
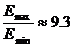
Оттук следва, че звездата в минимум е около 9 пъти по-слаба отколкото в максимум.
Амплитудата на изменение на звездната величина Δm намираме чрез формулата на Погсон:
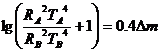
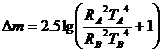
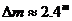
3 задача. Снаряд към Луната. В своя роман “Пътешествие към Луната” Жул Верн описва изстрелването на снаряд от огромно оръдие, вкопано в недрата на планината. Вие пътувате в този снаряд и вече сте в космоса. Виждате как нашата Земя става все по-малка, а Луната – по-голяма.
• На какво разстояние X от Земята за вас видимите ъглови диаметри на Луната и на Земята ще се изравнят?
• На какво разстояние Y от Земята силите, с които ще ви привличат Луната и Земята, ще станат равни?
• Защо според вас разстоянията Х и Y не са еднакви?
Считайте, че през цялото пътешествие се намирате на правата линия Земя-Луна. Разстоянието от Земята до Луната е 384 000 км. Диаметърът на Луната е 3470 км, на Земята 12740 км. Масата на Луната е 81 пъти по-малка от масата на Земята.

Решение:
Да означим с r разстоянието от Земята до Луната, а с DT и DL – линейните диаметри на Земята и Луната. Когато се отдалечим на разстояние Х от Земята, видимите ъглови диаметри на Земята и на Луната ще бъдат съответно:
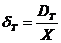 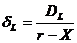
От равенството 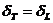 намираме: намираме:
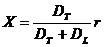
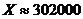 km km
Означаваме с MT и ML масите на Земята и Луната, с m масата на снаряда, а с γ гравитационната константа. Когато снарядът е на разстояние Y от Земята, силите, с които го привличат Земята и Луната, съгласно закона на Нютон, са следните:
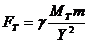 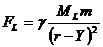
От равенството 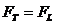 намираме: намираме:
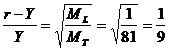
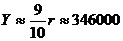 km km
Разстоянията X и Y не са еднакви, защото зависят от различни величини, свързани със Земята и Луната, като при това самите зависимости са различни. Видимите ъглови диаметри на Земята и Луната, от които се определя разстоянието X, са право пропорционални на линейните диаметри на двете тела и обратно пропорционални на разстоянията до тях. Гравитационните сили, действащи на снаряда от Земята и Луната, от които се определя разстоянието Y, са пропорционални на масите на двете тела и обратно пропорционални на квадратите на разстоянията до тях.
4 задача. Слънце на север. Откъде по Земята и кога можем да видим Слънцето на север? Разгледайте всички възможности и пояснете вашия отговор с подходящи схеми.
Решение:
Да видим Слънцето на север означава то, в определен момент от време, да пресича меридиана на мястото на север от зенита.
Очевидно решение изглежда южното полукълбо на Земята. Но и там Слънцето не навсякъде е на север през цялата година. В зоната между екватора и южната тропична окръжност съществува интервал от време, когато Слънцето се вижда на юг. Така например, в момента на зимното слънцестоене, когато Слънцето е в зенита за точка от южната тропична окръжност, от цялата зона между екватора и южната тропична окръжност Слънцето се вижда на юг от зенита. За останалите дати между есенното и пролетното равноденствие Слънцето е на север за места с южна географска ширина по-голяма, по абсолютна стойност, от моментната деклинация на Слънцето.
В лятното полугодие за северното полукълбо, т.е. между пролетното и есенното равноденствие, Слънцето е на север за цялото южно полукълбо и за места между екватора и северната тропична окръжност със северна ширина по-малка от моментната деклинация на Слънцето. В момента на лятно слънцестоене Слънцето е в зенита за точка от северната тропична окръжност и следователно е на север за всички точки на юг от нея.
На пръв поглед изглежда, че с това се изчерпват всички възможности, но не е така. На 22 юни, в деня на лятното слънцестоене, Слънцето не залязва за всяка точка от земната повърхност, намираща се на север от северната полярна окръжност. Като изключим северният полюс, където посоката „север“ не е дефинирана, от всички останали точки зад полярната окръжност Слънцето се вижда на север, над хоризонта, в момента на своята долна кулминация, т.е. в полунощ по местно слънчево време. През цялото лятно полугодие съществува зона от която Слънцето може да бъде видяно на север. Това са точки с географска ширина φ > 90° - δS , където δS е моментната деклинация на Слънцето.
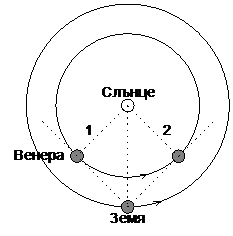
5 задача. Венера.На чертежа са показани орбитите на Земята и Венера около Слънцето. Когато Венера е в положение 1 спрямо Земята и Слънцето, казваме, че се намира в максимална източна елонгация, а когато е в положение 2 – в максимална западна елонгация.
• Защо когато Венера е около максимална източна или около максимална западна елонгация, условията на видимост на планетата за нас са най-благоприятни?
• На 14 януари 2009 г. Венера е била в максимална източна елонгация. В коя част на денонощието и приблизително в каква посока по небето се е виждала тя тогава?
• Кога най-скоро Венера ще бъде в максимална западна елонгация? Планетата обикаля около Слънцето с период 224.7 денонощия. Радиусите на орбитите на Венера и на Земята са приблизително в съотношение 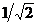 . .
Решение:
Трудността при наблюдението на вътрешните планети, каквато е Венера, е свързана с това, че те са близо до Слънцето и през голяма част от времето, гледани от Земята, те се губят на фона на светлото небе около Слънцето. В моментите на максимална източна или западна елонгация за земния наблюдател планетата е на най-голямо видимо ъглово отстояние от Слънцето и по тази причина се вижда най-добре. При всяко друго положение на Венера ъгълът Слънце-Земя-Венера е по-малък.
Въртенето на Земята около нейната ос е в същата посока, както нейното и на всички други планети движение около Слънцето. За земния наблюдател въртенето на Земята става от запад на изток. При максимална източна елонгация Венера е на изток от Слънцето. Сутрин Слънцето изгрява първо, а след него Венера. През деня е трудно да видим планетата в светлото небе, макар и в някои случаи да е възможно – тогава я наричат Деница. Но вечер, когато Слънцето залезе и небето стане достатъчно тъмно, над западния хоризонт се вижда ярко блестящата Венера. Тогава тя е Вечерница. Колкото по-голямо е видимото ъглово отстояние на Венера от Слънцето, толкова по-добре и по-дълго време след залеза му можем да видим планетата.
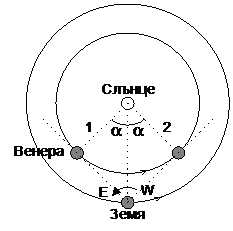
Тъй като радиусите на орбитите на Венера и Земята се отнасят приблизително както 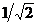 , ъгълът Земя-Слънце-Венера, означен на чертежа с a , е равен на около 45°. Венера е по-близо до Слънцето, отколокото Земята, и съгласно ІІІ закон на Кеплер, се движи по своята орбита по-бързо от нашата планета. За да определим колко време след максималната източна елонгация Венера ще бъде в максимална западна елонгация, трябва да намерим за колко време Венера при движението си около Слънцето ще “избърза” относно Земята на ъгъл , ъгълът Земя-Слънце-Венера, означен на чертежа с a , е равен на около 45°. Венера е по-близо до Слънцето, отколокото Земята, и съгласно ІІІ закон на Кеплер, се движи по своята орбита по-бързо от нашата планета. За да определим колко време след максималната източна елонгация Венера ще бъде в максимална западна елонгация, трябва да намерим за колко време Венера при движението си около Слънцето ще “избърза” относно Земята на ъгъл 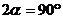 . Означаваме дадения ни орбитален период на Венера, който е сидеричният й период, с . Означаваме дадения ни орбитален период на Венера, който е сидеричният й период, с 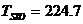 денонощия, а с денонощия, а с 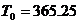 денонощия – орбиталния период на Земята. Пресмятаме синодичния период на Венера TSYN от формулата: денонощия – орбиталния период на Земята. Пресмятаме синодичния период на Венера TSYN от формулата:
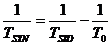
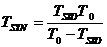
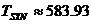 денонощия денонощия
За такъв период Венера прави една обиколка около Слънцето в координатна система с център Слънцето, в която Земята е неподвижна (или с други думи система, в която отсечката Земя-Слънце е неподвижна). Всъщност, ако умножим двете страни на равенството (1) по 360° или по 2p, то ще получим формула за относителната ъглова скорост на Венера спрямо Земята като разлика между абсолютната ъглова скорост на Венера при движението й около Слънцето и абсолютната ъглова скорост на Земята. Оттук можем да намерим за какво време t Венера ще “избърза” на ъгъл 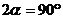 от Земята чрез следната пропорция: от Земята чрез следната пропорция:
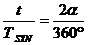
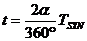
 дни дни
Сега трябва да определим и датата:
14 януари + 146 дни =
= 14 януари + 17 +28 + 31 + 30 + 31 + 9 дни от юни 2009г.
Следователно Венера ще бъде в максимална западна елонгация окло 9 юни 2009 г.
В действителност максималната западна елонгация на Венера е на 6 юни. Разликата се дължи на даденото приблизително отношение на радиусите на Венера и Земята и на елиптичността на земната орбита. |
|