|
МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ
ХІІІ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
ІІІ кръг
Ученици от 7-8 клас
ТЕОРЕТИЧЕН ТУР
Задача 1. Най-дългият рожден ден. Представете си, че имате приятел, който е роден на 29 февруари. Той трябва да празнува рождения си ден само веднъж на 4 години. Затова през предстоящата високосна 2012 година вие решавате да му устроите най-дългия рожден ден. Разполагате с достатъчно финансови средства, за да осъществите плана си, като пътешествате, където поискате.
• Как ще направите така, че рожденият ден на вашия приятел да продължи максимално дълго?
• Колко време може да продължи този рожден ден?
Решение:
За да направим по-дълъг рождения ден на 29 февруари, ще използваме различното време в различните часови пояси на Земята. Можем да постигнем това по два начина.
І начин. Линията на смяна на датите, или 180-градусовият меридиан, е централният меридиан на един особен часови пояс. В двете половини на този пояс от двете страни на 180-градусовия меридиан има две различни дати. Например, ако в западната половина на пояса датата е 29 февруари, то в източната е 28 февруари. Тръгваме на запад от 180-градусовия меридиан миг след полунощ, или 0 ч. по поясното време на 29 февруари. Ако след един час стигнем до границата със следващия часови пояс, то когато пресечем тази граница, за нас отново ще е миг след 0 ч. на 29 февруари по поясното време вече на новия часови пояс, в който се намираме. След още един час се озоваваме в още по-следващия часови пояс и пак е 0 ч. на 29 февруари. Така обикаляме цялата Земя и 24 часа след тръгването си сме пресекли 23 часови пояса и половина. Накрая се връщаме отново в часовия пояс, в който е линията на смяна на датите, но оставаме в източната половина на този пояс, защото на запад вече е 1 март. За нас сега обаче отново е миг след 0 ч. по поясно време на 29 февруари. След като сме се изморили от дългия път, оставаме през следващите 24 часа тук, докато настъпи пак полунощ и дойде датата 1 март. Така ние ще сме удължили рождения ден на нашия приятел до 48 часа. Можем да извършим това пътешествие със самолет по екватора или на други географски ширини, а може да отидем някъде около Северния или Южния полюс и да направим същото преминаване през часовите пояси, вървейки пеш по снега и леда.
ІІ начин. Като помислим внимателно върху основните идеи на първото решение, стигаме до извода, че можем да осъществим идеята дори и без да пътешестваме. Достатъчно е в 0 ч. по поясно време на 29 февруари да бъдем само на една крачка западно от 180-градусовия меридиан. (На изток от него е все още 28 февруари.) Трябва да сме на кораб, понеже този меридиан никъде не минава по суша, освен в Антарктида. Можем да седнем около празничната маса, или да си намерим други занимания, прекарвайки весело времето до секунда преди 0 ч. на 1 март. Тогава правим крачка на изток и сме от източната страна на линията на смяна на датите. Тук сега е 0 ч. на 29 февруари. Продължаваме да се забавляваме още 24 часа до 0 ч. на 1 март и така празнуваме рождения ден общо 48 часа.
2 задача. Планета в небето. Когато се наблюдават от Земята, планетите описват необикновени пътища на фона на звездното небе. Векове наред “примките”, които описват планетите, са озадачавали астрономите, особено онези от тях, които са били привърженици на геоцентричната система. На фигурата виждате видимия път на една планета за определен период от време. Това е всъщност карта на част от звездното небе, но самите звезди не са нанесени, за да не се усложни фигурата. Разгледайте внимателно всички данни върху нея и обърнете внимание в рамките на каква област от небето е ставало видимото преместване на планетата за отбелязания интервал от време.
• Направете необходимите пресмятания и определете коя е планетата.
Таблица 1. Средни разстояния до Слънцето (а) в астрономически единици и орбитални периоди (Т) в години на планетите от Слънчевата система.
Планета |
Меркурий |
Венера |
Земя |
Марс |
a , AU |
0.387 |
0.723 |
1 |
1.524 |
T , год. |
0.241 |
0.615 |
1 |
1.88 |
Планета |
Юпитер |
Сатурн |
Уран |
Нептун |
a , AU |
5.204 |
9.584 |
19.187 |
30.021 |
T , год. |
11.87 |
29.67 |
84.0 |
164.5 |
Решение:
Сложните линии, които описват планетите при видимото си движение на фона на звездното небе, се дължат на това, че ние ги наблюдаваме от движещата се около Слънцето Земя. На фигурата виждаме, че за две години – от началото на 1929 до началото на 1931 г. – видимото положение на планетата се е променило само с около 20°. Това означава, че планетата е сравнително далечна и се движи бавно около Слънцето. Определено това е външна планета.
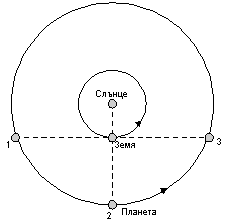
Фиг. 1.
Характерните конфигурации на външна планета по отношение на Слънцето за земен наблюдател са показани на Фиг. 1. С 1 и 3 са означени източната и западната квадратури, а с 2 – противостоенето. Известно време след като планетата е в източна квадратура, започва нейното обратно, или ретроградно видимо движение на фона на звездното небе. Съответното видимо положение на планетата е означено с точка 1' на Фиг. 2. На същата фигура с точки 2' и 3' са означени видимите положения на планетата по небето съответно в противостоене и известно време преди западна квадратура, когато завършва ретроградното движение.
На Фиг. 2 виждаме, че в интервала от време две години е имало два цикъла с източна квадратура, противостоене и западна квадратура на планетата.
След като веднъж планетата е била в противостоене, до следващото противостоене Земята трябва да направи една обиколка около Слънцето. След една обиколка на Земята обаче, планетата ще се е придвижила в друго положение по своята орбита. Планетата се движи по-бавно от Земята и нашата планета ще я “догони” след определено време. Така следващото противостоене на планетата се случва в положение по нейната орбита, което е отклонено на някакъв ъгъл α от предишното (Фиг. 3). Гледано от Земята, съответно, видимото положение на планетата на фона на звездите ще е отместено на същия ъгъл спрямо предното противостоене.
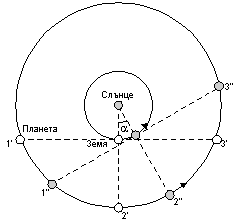
Фиг. 3
Тъй като планетата е далечна и се движи доста бавно, то можем приблизително да смятаме, че за една земна година тя изминава ъгъл α от своята орбита. Така за орбиталния период на планетата, изразен в земни години, получаваме:
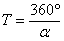
За да определим ъгъла α от Фиг. 2 не е удобно да работим с точките на противостоене, тъй като е трудно да ги определим точно. Нека изберем източните точки на обръщане 1' и 1''. Спускаме перпендикуляри от тези точки към еклиптиката и определяме разликата между техните еклиптични дължини. Първо измерваме мащаба по хоризонталната скала и получаваме, че на ъгъл 20° съответстват 118.5 мм. За разликата между еклиптичните дължини на точките 1' и 1'' получаваме:
α = 67.5 мм × 20° / 118.5 мм ≈ 11.4°
За по-голяма точност по принцип можем да определим и разликата между еклиптичните дължини на точките 3' и 3' и после да усредним резултата, но при измерването той се оказва точно същият. За орбиталния период на планетата намираме:
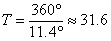 години години
От Таблица 1 с данните за планетите виждаме, че тази стойност е най-близка до орбиталния период на Сатурн. Следователно планетата, чиито видим път е показан на фигурата, е Сатурн.
3 задача. Астероидът В612. Космически пътешественик странства със своя кораб из Слънчевата система. В даден момент през телескопа си той вижда астероида на Малкия принц, както е представен на рисунката. В зрителното поле попадат също Слънцето и Сатурн.
• Кое е по-голямо – радиусът на орбитата на астероида В612 около Слънцето или радиусът на орбитата на Сатурн? Отговорете само качествено и обяснете вашия отговор.
• Колко пъти разстоянието от кораба на пътешественика до Слънцето е по-голямо или по-малко от разстоянието от кораба до Сатурн? Направете необходимите измервания и пресмятания.
• Да предположим, че в момента на наблюдението Сатурн е бил в противостоене за наблюдател, намиращ се на Земята. При такова условие къде космическият пътешественик би виждал Земята? Нанесете видимото положение на Земята върху рисунката.
Диаметърът на Сатурн е 120 500 км, а на Слънцето – 1390000 км. Считаме, че астероидът и Сатурн се движат около Слънцето по кръгови орбити.
Решение:
Измерваме диаметрите на Слънцето и Сатурн върху рисунката и получаваме съответно 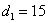 мм и мм и 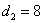 мм. Следователно видимите ъглови диаметри на Слънцето и Сатурн от позицията на космическия пътешественик са в съотношение 15/8 ≈ 1.88. Но ние знаем, че действителният диаметър на Сатурн в километри е доста пъти по-малък отколкото този на Слънцето. Оттук заключаваме, че в момента на наблюдението планетата Сатурн се намира значително по-близо до космическия пътешественик, отколкото Слънцето. Същевременно се убеждаваме, че видимото ъглово отстояние между Слънцето и Сатурн е твърде малко. Достатъчно е само да го сравним с видимите ъглови размери на самите тези обекти. Освен това, предвид големите видими размери на астероида В 612, очевидно той е много по-близо до космическия пътешественик, отколкото Сатурн или Слънцето. Общо взето, разположението на обектите изглежда така: мм. Следователно видимите ъглови диаметри на Слънцето и Сатурн от позицията на космическия пътешественик са в съотношение 15/8 ≈ 1.88. Но ние знаем, че действителният диаметър на Сатурн в километри е доста пъти по-малък отколкото този на Слънцето. Оттук заключаваме, че в момента на наблюдението планетата Сатурн се намира значително по-близо до космическия пътешественик, отколкото Слънцето. Същевременно се убеждаваме, че видимото ъглово отстояние между Слънцето и Сатурн е твърде малко. Достатъчно е само да го сравним с видимите ъглови размери на самите тези обекти. Освен това, предвид големите видими размери на астероида В 612, очевидно той е много по-близо до космическия пътешественик, отколкото Сатурн или Слънцето. Общо взето, разположението на обектите изглежда така:

Разбира се, тази схема е много приблизителна. Но от нея става ясно, че Сатурн е по-близо до Слънцето, отколкото В612 и радиусът на орбитата на Сатурн е по-малък от радиуса на орбитата на астероида.
Означаваме с r1 и r2 разстоянията от космическия пътешественик съответно до Слънцето и до Сатурн, с δ1 и δ2 видимите ъглови размери на Слънцето и Сатурн, а с D1 и D2 – техните линейни диаметри в километри. Видимият ъглов диаметър на Слънцето е пропорционален на неговия линеен диаметър и обратно пропорционален на разстоянието от наблюдателя до него. Същото се отнася и за Сатурн. Следователно можем да напишем:
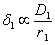 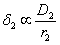
(В случай, че видимите ъглови размери се измерват в радиани, това са истински равенства). Измерените на рисунката размери на изображенията на Слънцето и на Сатурн d1 и d2 са в същото съотношение, в каквото са и техните видими ъглови размери. Оттук получаваме:
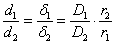
В задачата се търси съотношението на разстоянията до Слънцето и Сатурн. От горното уравнение намираме:

Накрая получаваме:
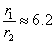
Сатурн е около 6 пъти по-близо до космическия пътешественик, отколкото Слънцето.
Когато за земния наблюдател Сатурн е в противостоене, Земята се намира между Слънцето и Сатурн и Сатурн за нас е в посока, диаметрално противоположна на Слънцето. Тогава разстоянието от Земята до Сатурн ще бъде с една астрономическа единица по-малко, отколкото разстоянието то Слънцето до Сатурн. Използвайки данните от таблицата в задача 2, намираме, че разстоянието Земя – Сатурн ще бъде 9.584 –1 = 8.584 AU, или приблизително 8.6 пъти по-голямо от разстоянието Земя – Слънце. В същото съотношение трябва да са и видимите на рисунката разстояния, понеже те са проекция под някакъв ъгъл на истинските разстояния между обектите. Съединяваме центровете на Слънцето и Сатурн с отсечка. Делим я на две части в съотношение 1:8.6 и така намираме видимото положение на Земята.
ПРАКТИЧЕСКИ ТУР
Протуберанс. На 6 март 1999 космическата слънчева обсерватория SOHO прави серия от снимки, на които се вижда развитието на един протуберанс. Разполагате с шест изображения, получени в рамките на 1 час и 10 минути. На всяко едно от тях е отбелязана датата и точното време в UT. Изображенията са квадратни със страна 10 дъгови минути. На 6 март космическата обсерватория е била на 0.99 AU от Слънцето.
• Сравнете размерите на протуберанса и Земята. На последното изображение нарисувайте Земята в правилния мащаб.
• Измерете височините на протуберанса над слънчевия диск и постройте графика на изменението им с времето. Изчислете скоростта на протуберанса. Променя ли се тя с времето?
Справочни данни:
Радиус на Земята – 6370км
1AU (Астрономическа единица ) – 150 000 000 км
Решение. Линейният размер на изображенията е 82 мм. Следователно ъгловият мащаб е k = 10/82 = 0.122 arcmin/мм. На разстояние r = 0.99 AU = 148500000 км Земята би имала ъглов диаметър dЗ = 206265.D/r = 17''.7 (дъгови секунди) = 0'.295 (дъгови минути), където D = 2RЗ е диаметърът на Земята. За да получим диаметъра на Земята в мащаба на снимките, трябва ъгловия размер да разделим на ъгловия мащаб на изображенията:
dЗ мм = dЗ / k= 2.42 мм. Виждаме, че на последното изображение протуберансът е почти 20 пъти по-голям от Земята.
Измерваме височината на протуберанса над слънчевия диск в милиметри за всяко едно изображение. Умножаваме по ъгловия мащаб и получаваме височината в дъгови минути. За да получим линейния размер на протуберанса в километри, трябва да преминем от ъглови единици към линейни (в реален мащаб). Мащабният коефициент може да получим от ъгловите и реални линейни размери на Земята: k' = D/ dЗ = 43186 км на дъгова минута. Умножаваме ъгловите размери на протуберанса по коефициента и получаваме реалните му линейни размери в километри.
Разбира се, може да построим общ преходен коефициент и да преминаваме от милиметри на изображенията към истински размери в километри.
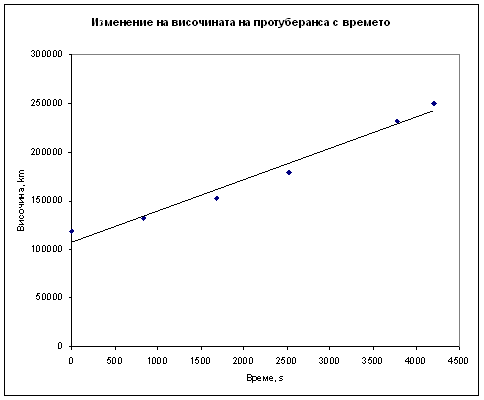
Резултатите от пресмятанията са дадени в таблицата.
В първата колона е времето Δt в секунди, изминало от началния момент.
Δt,
s |
Височина на протуберанса
върху изображението
мм |
Ъглови размери на протуберанса
arcmin |
Линейни размери на протуберанса
км |
Средна скорост за интервала
km/s |
0 |
22.5 |
2.745 |
118546 |
|
840 |
25 |
3.05 |
131717 |
15.7 |
1681 |
29 |
3.538 |
152792 |
25.1 |
2520 |
34 |
4.148 |
179136 |
31.4 |
3781 |
44 |
5.368 |
231822 |
41.8 |
4200 |
47.5 |
5.795 |
250263 |
44.0 |
Тук средната скорост е изчислена за средата на интервала време, но е записана в реда на крайния момент на интервала. Начертаваме графика на изменението на скоростта с времето. Общата средна скорост на протуберанса е малко над 30 km/s . От графиката обаче, баче ясно се вижда тенденция към растене на скоростта с времето.
|
|