МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ
ХІІ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
ІІІ кръг
Ученици от 9-10 клас
ТЕОРЕТИЧЕН ТУР
Задача 1. Вие членувате в клуб на смелите пътешественици със странни идеи. Решили сте да направите пътуване по суша и море, като се движите само по гринуичкия меридиан. Ориентирате се по звездите. Наблюдавате звездата Феркад (γ Малка мечка) с деклинация 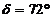 и измервате нейната височина в горна кулминация. Оказва се, че всеки ден височината й е с 1° по-голяма отколкото предния ден. В каква посока се движите? С каква скорост? и измервате нейната височина в горна кулминация. Оказва се, че всеки ден височината й е с 1° по-голяма отколкото предния ден. В каква посока се движите? С каква скорост?
На 9 май Феркад се наблюдава в горна кулминация около 0 h по гринуичко време. Приблизително каква е ректасцензията на звездата?
В колко часа по гринуичко време ще видите Феркад в горна кулминация на 10 май?
Решение:
Деклинацията на Феркад е 72°. При видимото си движение по небето тя описва денонощния паралел aa' с радиус 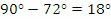 . На различни географски ширини са възможни различни случаи. Може в горна кулминация звездата да е на юг, както е на схема 1). Височината на звездата над хоризонта в горна кулминация се измерва от точката S на хоризонта до a'. . На различни географски ширини са възможни различни случаи. Може в горна кулминация звездата да е на юг, както е на схема 1). Височината на звездата над хоризонта в горна кулминация се измерва от точката S на хоризонта до a'.
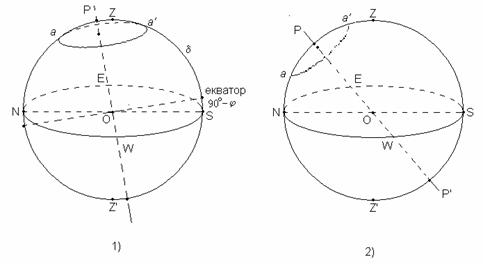
Тогава, ако с всеки следващ ден височината над хоризонта на звездата в горна кулминация е по-голяма, клубът на пътешествениците се движи на юг – вследствие на това северният небесен полюс P се отклонява все повече и повече от зенита за наблюдателя и точката, в която Феркад кулминира, се вдига все по-високо над хоризонта. Това е валидно за географска ширина φ на наблюдателя, за която:
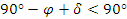 или или 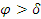
Тук δ е деклинацията на Феркад.
Възможно е, обаче, Феркад да бъде в горна кулминация на север, както ни убеждава схема 2). В този случай височината на звездата над хоризонта в горна кулминация се измерва от точката N на хоризонта до a?. Сега ако пътешествениците наблюдават увеличаване на височината над хоризонта на Феркад в горна кулминация, те се движат на север. Така става, когато 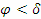 . Накрая нека не забравяме, че когато пътешествениците навлязат достатъчно на юг в южното полукълбо, то те няма да виждат Феркад над хоризонта. . Накрая нека не забравяме, че когато пътешествениците навлязат достатъчно на юг в южното полукълбо, то те няма да виждат Феркад над хоризонта.
Щом височината на звездата се увеличава с 1° на ден, с толкова се променя и географската ширина на пътешествениците. Дължината s на дъга от един градус по земната повърхност можем да изчислим примерно така:
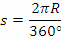
където R е земният радиус. За скоростта на пътешествениците получаваме:
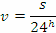
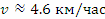
Звездата е в горна кулминация на 9 май в полунощ. Тогава Слънцето е на 180°, или 12h от звездата по ректасцензия. Да намерим ректасцензията на Слънцето. Датата 9 май е определен брой дни след пролетното равноденствие на 21 март:
10 (от март) + 30 (април) + 9 (май) = 49 дни
При пролетното равноденствие Слънцето е имало ректасцензия, равна на 0. На 9 май тя е:
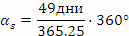

Така за ректасцевзята на звездата получаваме:
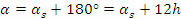
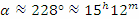
Периодът между две горни кулминации на една звезда е равен на звездното денонощие, или 23h56m. Ако звездата е била в горна кулминация на 9 май в 0 h по гринуичко време, то следващата й горна кулминация ще бъде в 23h56m все още на 9 май. На 10 май ще се случи едва по-следваща горна кулминация на звездата и тя ще бъде в 23h52m по гринуичко време.
Задача 2. Вие сте придворен астроном при велик марсиански владетел. Наблюдавате спътниците Фобос и Деймос с цел да усъвършенствате марсианската календарна система.
В каква посока ще става видимото денонощно движение на Фобос и Деймос по марсианското небе?
За времето между два изгрева на Деймос колко изгрева на Фобос ще се наблюдават?
Ако Фобос е във фаза “пълнолуние” в момента на своя изгрев, приблизително в каква фаза ще е при следващия си изгрев? А Деймос?
Ще бъде ли лесно да се състави марсиански лунен календар?
Решение:
Двата спътника на Марс се движат около планетата в същата посока, в която става и околоосното й въртене. Веднага виждаме, че орбиталният период да Фобос TF е по-кратък от периода на околоосно въртене на Марс TM . Това означава, че за наблюдател на марсианската повърхност Фобос ще изгрява от запад и ще залязва на изток. Орбиталният период на Деймос TD е по-дълъг от TM , така че Деймос ще изгрява от изток и ще залязва на запад. Нека времената между два изгрева на Фобос и на Деймос са съответно TF’ и TD’. В сила са следните съотношения:
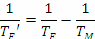
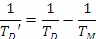
От тях получаваме:
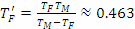 денонощия денонощия
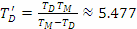 денонощия денонощия
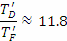
Получава се, че за времето между два изгрева на Деймос Фобос може да изгрее 11 пъти!
Периодите между две пълнолуния на Фобос и на Деймос можем да намерим, като използваме орбиталния период на Марс около Слънцето, който не ни е даден. Ние обаче знаем, че той е около 2 години. Орбиталният период на Марс е твърде дълъг в сравнение с кратките периоди на движение на Фобос и Деймос около Марс. Затова разликата между сидеричния и синодичния „месец” за всеки от двата спътника е много малка и ще я пренебрегнем.
След като Фобос е изгрял във фаза пълнолуние, то за да разберем в каква фаза ще е при следващия си изгрев, пресмятаме:
TF/TF' ≈ 1.452
TD/TD' ≈ 1.348
При следващия си изгрев Фобос ще бъде приблизително във фаза новолуние, а Деймос ще бъде на възраст около една трета от синодичния си период след пълнолуние.
Множество интересни съотношения се получават между различните периодични явления, свързани със спътниците. Но те са твърде сложни и недостатъчно съотношения на малки цели числа. Затова съставянето на марсиански лунен календар би било много трудно.
Задача 3. В последно време астрономите откриват множество планети около други звезди. В сравнение с планетите от родната ни Слънчева система, преобладаващата част от тези далечни планети са твърде необикновени. Една такава планета е открита около звездата WASP 4. Звездата е от спектрален клас G7, с температура 5500 К и радиус 1.15 слънчеви радиуса. Намира се на 300 парсека от нас. Планетата е с маса 1.12 пъти по-голяма от масата на Юпитер и обикаля около звездата на разстояние само 0.023 астрономически единици с период 1.3382 земни денонощия.
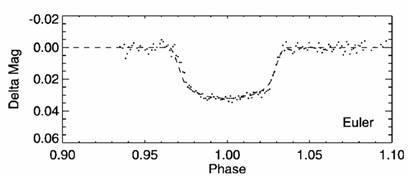
Графиката показва изменението на блясъка на звездата по време на наблюдаван пасаж на планетата по диска на звездата. Използвайте данните от графиката и определете радиуса на планетата. Направете това по два начина и сравнете получените от вас резултати. Коментирайте разликите.
При пасажа планетата преминава приблизително през центъра на видимия диск на звездата. По вертикалната скала е нанесена не самата видима звездна величина на звездата, а нейното изменение спрямо стойността, която има извън времето на пасажа.
Решение: Намаляването на блясъка на звездата се дължи на това, че планетата застава между нея и наблюдателя като засенчва част от светлината. Когато планетата не е пред звездата, осветеността Eo , която звездата създава на Земята, е пропорционална на πRзв2 , където Rзв е радиусът на звездата:
Еo ~ πRзв2
Когато планетата е пред звездата светлина идва само от тази част от звездата, която не е засенчена от диска на планетата:
Е1 ~ π( Rзв2 – Rпл2 )
От формулата на Погсон:
Еo / Е1 = 2.512Δm
Rзв2/ (Rзв2 – Rпл2) = 2.512Δm
Rпл = Rзв (1 – 1/2.512Δm )1/2
Измерваме амплитудата на изменение на блясъка и получаваме: Δm = 0.032m
Пресмятаме и получаваме за Rпл: Rпл = 0.17Rзв≈ 140000 km
Вторият начин за определяне на размерите на звездата е свързан с геометрията на затъмнението. Затъмнението започва, когато дискът на планетата започне да засенчва диска на звездата. Максимална фаза настъпва, когато целият диск на планетата застане пред диска на звездата. Следва плосък минимум докато дискът на планетата не достигне срещуположния край на диска на звездата. Следва край на затъмнението в обратен ред. В пълна фаза обикновенно се наблюдава известна заобленост на минимума. Тя се дължи на потъмнението към края на диска на звездата. Основните моменти на затъмнението схематично са показани на фигурата.
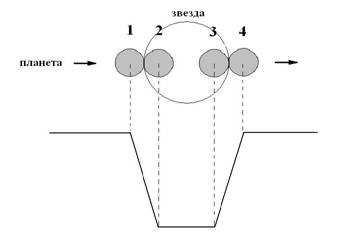
Ширината в горната част на минимума е равна на:
L1 = 2(Rзв + Rпл)
Ширината в долната част на минимума плюс интервалът на покачване на блясъка е:
L2 = 2Rзв
Делим първия израз на втория и получаваме:
L1/L2 = 1 + Rпл /Rзв
Rпл = (L1/L2 – 1 )Rзв = 0.17Rзв ≈ 140000 km
Виждаме, че двата метода водят до еднакви или близки резултати.
Справочни данни:
Радиус на Земята 6370 км;
Радиус на Слънцето 700000 км
Орбитален период на Фобос – 0.31891 земни денонощия
Орбитален период на Деймос – 1.26244 земни денонощия
Период на околоосно въртене на Марс – 1.02595 земни денонощия
ПРАКТИЧЕСКИ ТУР
Планета около Фомалхаут.
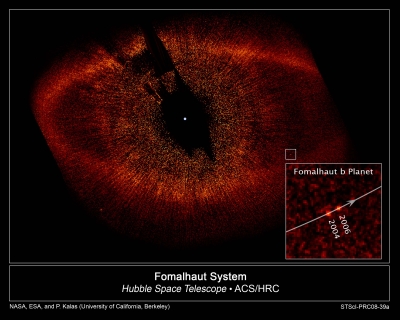
Разполагате с негативно изображение на малка област около звездата Фомалхаут – a Южна риба. Самата звезда е засенчена с екран, чиято сянка се вижда на изображението. На снимката се вижда пръстен от прах недалеч от вътрешната страна на който е открита планета. Тя е в малкия квадрат отдясно под който е изобразен същият квадрат, но в уголемен размер. В големия квадрат са отбелязани две положения на планетата. В тях тя е била заснета директно с телескоп през 2004 и 2006 години. Освен това на изображението са показани посоките по небесната сфера и е дадена мащабна отсечка. Направете необходимите измервания и пресметнете масата на Фомалхаут. Представете я в слънчеви маси.
Масата на Слънцето е 2×1030 kg.
Решение:
Пръстенът от прах има форма близка до елипса. Фомалхаут, обаче, се намира недалеч от центъра на елипсата, а не в някой от фокусите й. Това означава, че елипсата е проекция върху небесната сфера на почти кръгов пръстен близо до центъра на който се намира Фомалхаут. Положението на планетата е неблагоприятно за директно определяне на разстоянието й до звездата. Тя е в посока към нас и надясно. Знаейки, че елипсата е проекция на кръг, измерваме разстоянието r1 от центъра (от Фомалхаут) до планетата и по същия радиус – до праховия пръстен разстоянието r01. Получаваме r1 = 82 mm и r01 = 97 mm. Истинският радиус на пръстена може да намерим като измерим голямата полуос на елипсата. Измерваме наляво до най-издадената част на елипсата r02 = 105 mm. Ако си представим, че планетата е разположена наляво, по протежение на отсечката r01 , то разстоянието до нея ще бъде:
r2 = r1 (r02 /r01 ) = 89 mm
Да пресметнем в астрономически единици. Мащабната отсечка е дълга 75 mm. На тях отговарят 100 AU. Мащабът е:
k = x [AU] / x [mm] = 100/75 = 1.333 AU/mm
Пресмятаме:
r2 [AU] = 119 AU
Измерваме размерите на двата квадрата и виждаме, че отношението в линейните им размери е 10. Измерваме разстоянието между изображенията на планетата в големия квадрат. Получаваме y1 = 9.5 mm. Тогава в малкият квадрат и следователно в основното изображение, това разстояние трябва да е y2 = 0.95 mm. Това разстояние, обаче, не можем да превърнем веднага в астрономически единици – AU. Причината за това е, че виждаме отсечката, съединяваща двете положения на планетата, в ракурс. По тази причина видимото разстояние между тях е по-малко от истинското. За да видим какво е истинското разстояние трябва да ги разположим в плоскост перпендикулярна на лъча на зрение. За тази цел ще завъртим равнината в която те се намират до ъгъл 90° към лъча на зрение (Виж фигурата).
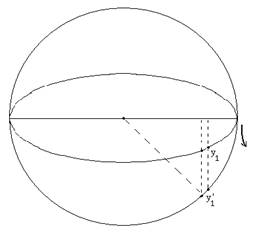
Тъй като голямата ос на елипсата е перпендикулярна на лъча на зрение при завъртането хоризонталният размер на дъгичката на изминатия от планетата път няма да се промени.
На практика това става, като нарисуваме вероятната орбита на планетата (или част от нея), от вътрешната страна на праховия пръстен, като вземем предвид леката изтегленост на пръстена надясно, така както би изглеждала, ако лъчът на зрение би бил перпендикулярен на равнината на орбитата.
Построяваме част от орбитата на планетата върху изображението, в двете ориентации. Пренасяме успоредно в големия квадрат. Отбелязваме вероятните положения на планетата. Измерваме y1' и получаваме:
y1' = 12.5 mm
В мащаба на основното изображение:
y2' = y1' / 10 = 1.25 mm
В астрономически единици:
y2' [AU] = k · y2' = 1.67 AU
Това разстояние е изминато от планетата за t2 = 2 години. Поради това, че планетата се движи почти по кръгова орбита, използваме формулата за първа космическа скорост. От нея следва:
vI = y2' / t2 = (γM/r2 )1/2
С е γ означена гравитационната константа, а с М - масата на Фомалхаут.
M = (r2 /γ)( y2' /t2)2
M = 4.2 ×1030 kg
M = 2.1 слънчеви маси |