|
МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ
ХІІІ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
ІІІ кръг
Ученици от 9-10 клас
ТЕОРЕТИЧЕН ТУР
Задача 1.
Тихо Брахе. Забележителният датски астроном Тихо Брахе е извършвал многогодишни систематични наблюдения на планетите. Той е създател на най-точните наблюдателни инструменти в епохата преди изобретяването на телескопа.
Като не споделял напълно геоцентричната система, Тихо Брахе считал, че планетите обикалят около Слънцето. Но Земята според него, все пак е неподвижна и Слънцето заедно с планетите се движи около нея.
• Тихо Брахе е бил готов да приеме хелиоцентричната система на Коперник, но е бил озадачен от липсата на един наблюдаем ефект, който би потвърдил движението на самата Земя. Какъв е бил този ефект?
Тихо Брахе е разсъждавал какво би следвало от предположението, че Земята наистина се движи около Слънцето, а гореспоменатият ефект не може да се наблюдава, понеже е твърде малък за тогавашната точност на измерванията (една дъгова минута). В писмо до свой колега астроном той пише: „Считаш ли за възможно разстоянието между Слънцето и Сатурн да не съставлява и 1/700 част от разстоянието до сферата на неподвижните звезди? .... А тогава и неподвижните звезди от трета звездна величина, видимият диаметър на които е равен на една минута, трябва да имат размерите на ......” (По времето на Тихо Брахе все още се е считало, че звездната величина се определя от видимия размер на звездите).
• Какво трябва да е минималното разстояние до “сферата на неподвижните звезди” според разсъжденията на Тихо Брахе?
• Имал ли е той добра представа за разстоянието между Слънцето и Сатурн?
• Запълнете пропуснатото в края на цитата от писмото на Тихо Брахе.
• С какви други наблюдения с наземни телескопи може да се докаже движението на Земята около Слънцето?
Решение:
При точност до една дъгова минута не би могло да се установи и измери паралактичното отместване на по-близките звезди на фона на по-далечните, което се дължи на движението на Земята по нейната орбита около Слънцето. Както е известно, дори и за най-близката звезда паралаксът, съответстващ на видимия от звездата радиус на земната орбита, е по-малък от една дъгова секунда. Наблюдението на това явление твърдо би убедило Тихо Брахе, че Земята не е неподвижна, а обикаля около Слънцето. Тихо Брахе очевидно е бил наясно, че е възможно Земята наистина да се движи около Слънцето, но паралактичното отместване на звездите да не се забелязва, понеже зведите са на много големи разстояния. Това, което е поразявало Тихо Брахе, както личи от писмото, е колко всъщност огромни трябва да са тези разстояния в сравнение с тогавашните представи за мащабите на Вселената. Минималното разстояние, на което трябва да са най-близките звезди, за да не може да се забележи паралактичното им отместване, е разстоянието, при което диаметърът на земната орбита се вижда под ъгъл една дъгова минута. С други думи, радиусът на земната орбита трябва да се вижда от такива звезди под ъгъл 30 дъгови секунди и според съвременното определение това е нейният паралакс. Тъй като при паралакс една дъгова секунда разстоянието до звездата е един парсек, то при 30 пъти по-голям паралакс разстоянието до най-близките звезди би трябвало да бъде 1/30 част от парсека. Като знаем, че в един парсек има приблизително 206265 астрономически единици, получаваме, че най-близките звезди трябва да са на разстояние:
206265 / 30 ≈ 6880 астрономически единици
От таблицата с данните за планетите виждаме, че според съвременните данни Сатурн е отдалечен на разстояние от Слънцето около 9.5 астрономически единици. Това е
6880 / 9.5 ≈ 720 пъти по-малко от разстоянието до най-близките зведи, получено по-горе. Оценката на Тихо Брахе е около 700 пъти, което означава, че той е имал доста точна представа за разстоянието от Слънцето до Сатурн в астрономически единици. (Проблемът в онези времена е бил, че не е било известно със задоволителна точност самото разстояние от Земята до Слънцето, т.е. самата стойност на астрономическата единица).
Тихо Брахе е считал, че видимият от Земята ъглов размер на една звезда от трета звездна величина е една дъгова минута. Ако тази звезда е на оцененото от него минимално разстояние, то от нея диаметърът на земната орбита трябва да се вижда под ъгъл една дъгова минута. Следователно самата звезда трябва да има размерите на земната орбита. Пропуснатите думи в края на изречението на Тихо Брахе са “земната орбита”.
При наблюдения с наземни телескопи освен паралактичното отместване, може да се наблюдава и друг вид видимо отместване на небесните обекти, дължащо се на аберацията на светлината. Поради обикалянето на Земята около Слънцето се наблюдават също и изменения с период една година на лъчевите скорости на звездите и също – изменения с период една година на периодите на много циклични явления при космическите обекти.
2 задача. Планети в небето. Когато се наблюдават от Земята, планетите описват необикновени пътища на фона на звездното небе. Векове наред “примките”, които описват планетите, са озадачавали астрономите, особено онези от тях, които са били привърженици на геоцентричната система. На фигурата виждате видимите пътища на две планети за определен период от време. Това са всъщност карти на части от звездното небе, но самите звезди не са нанесени, за да не се усложни фигурата.
• Направете необходимите пресмятания и определете кои са планетите.
• В определени периоди от време планетите имат обратно или т.нар. ретроградно движение на фона на звездите – връщат се за малко назад от общата посока на видимо движение. За различните планети интервалите от време Δt, през които те имат ретроградно движение, са с различна продължителност. Каква ще бъде стойността на Δt за космически обекти, които са много по-далеч от Слънцето, отколкото най-далечните планети?
Решение:
Сложните линии, които описват планетите при видимото си движение на фона на звездното небе, се дължат на това, че ние ги наблюдаваме от движещата се около Слънцето Земя.
На горната фигура виждаме, че планетата се движи доста бързо на фона на звездите и прави едно пълно видимо завъртане приблизително за една година. Следователно това е някоя от вътрешните планети – Венера или Меркурий.
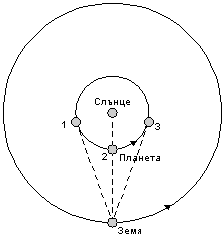
Фиг. 1
Характерните конфигурации на вътрешна планета по отношение на Слънцето за земен наблюдател са показани на Фиг. 1. С 1 и 3 са означени източната и западната елонгации, а с 2 – долното съединение.
Известно време след като планетата е в източна елонгация (по принцип при венера този интервал от време е доста съществен), започва нейното обратно, или ретроградно видимо движение на фона на звездното небе. Съответното видимо положение на планетата е означено с точка 1' на Фиг 2. С точка 2' е означено видимото положение на планетата по небето съответно известно време преди западна елонгация, когато завършва ретроградното движение.
Виждаме, че през юли 1932 г. и март 1934 е имало два цикъла с ретроградно движение. Между тях са минали около 22 месеца и това е приблизителна оценка на синодичния период на планетата. От таблиците с данните за планетите виждаме, че синодичните периоди на Меркурий и Венера са съответно около 111 и 583 дни. Оттук заключаваме, че планетата, чиито видим път е изобразен на горната графика, е Венера.
До същото заключение още по-бързо можем да достигнем, като сравним ъгловите отклонения от еклиптиката, до които достига планетата при своето видимо движение на горната схема и наклоните на орбитите на планетите, дадени в таблицата с данни.
На долната фигура виждаме, че за две години – от началото на 1929 до началото на 1931 г. – видимото положение на планетата се е променило само с около 20°. Това означава, че планетата е сравнително далечна и се движи бавно около Слънцето. Определено това е външна планета.
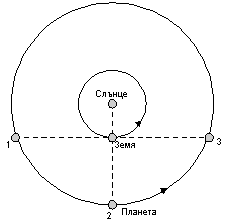
Фиг. 3.
Характерните конфигурации на външна планета по отношение на Слънцето за земен наблюдател са показани на Фиг. 3. С 1 и 3 са означени източната и западната квадратури, а с 2 – противостоенето.
Известно време след като планетата е в източна квадратура (по принцип при Марс това връме е съществено, но за далечна планета би било малко), започва нейното обратно, или ретроградно видимо движение на фона на звездното небе. Съответното видимо положение на планетата е означено с точка 1' на Фиг. 3. На същата фигура с точки 2' и 3' са означени видимите положения на планетата по небето съответно в противостоене и малко преди западна квадратура, когато завършва ретроградното движение.
На Фиг. 4 виждаме, че в обхванатия интервал от време е имало два цикъла с източна квадратура, противостоене и западна квадратура на планетата.
След като веднъж планетата е била в противостоене, до следващото противостоене Земята трябва да направи една обиколка около Слънцето. След една обиколка на Земята обаче, планетата ще се е придвижила в друго положение по своята орбита. Планетата се движи по-бавно от Земята и нашата планета ще я “догони” след известно време (Фиг.5). Така следващото противостоене на планетата се случва в положение по нейната орбита, което е отклонено на някакъв ъгъл a от предишното. Гледано от Земята, съответно, видимото положение на планетата на фона на звездите ще е отместено на същия ъгъл спрямо предното противостоене.
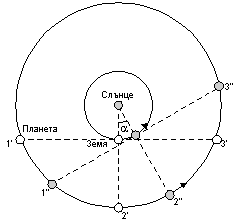
Фиг. 5
Тъй като планетата е далечна и се движи доста бавно, то можем приблизително да смятаме, че за една земна година тя изминава ъгъл α от своята орбита. Така за орбиталния период на планетата, изразен в земни години, получаваме:
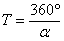
За да определим ъгъла α от Фиг. 2 не е удобно да работим с точките на противостоене, тъй като е трудно да ги определим точно. Нека изберем източните точки на обръщане 1' и 1''. Спускаме перпендикуляри от тези точки към еклиптиката и определяме разликата между техните еклиптични дължини. Първо измерваме мащаба по хоризонталната скала и получаваме, че на ъгъл 20° съответстват 118.5 мм. За разликата между еклиптичните дължини на точките 1' и 1'' получаваме:
α = 67.5 мм × 20° / 118.5 мм ≈ 11.4°
За по-голяма точност по принцип можем да определим и разликата между еклиптичните дължини на точките 3' и 3' и после да усредним резултата, но при измерването той се оказва точно същият. За орбиталния период на планетата намираме:
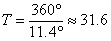 години години
От таблицата с данните за планетите виждаме, че тази стойност е най-близка до орбиталния период на Сатурн. Следователно планетата, чиито видим път е показан на фигурата, е Сатурн.
Колкото по-далеч от Слънцето се намира даден обект, принадлежащ към Слънчевата система, толкова по-бавно се движи той около Слънцето. Освен това, от по-далечно разстояние видимото ъглово преместване на обекта, дължащо се на собственото му движение, ще е все по-малко. Така че, определящо при видимото му движение ще бъде влиянието на орбиталното движение на Земята. Обектът ще описва все по-плътна поредица от примки, всяка от които ще се описва за около една земна година. Следователно, интервалът от време, през което обектът ще има ретроградно движение, ще се добилжава все повече до половин земна година.
3 задача. Геостационарна станция. Космическа станция се намира на геостационарна орбита около Земята. Към нея се изпращат доставки за екипажа с товарен кораб, който се движи около Земята по междинна елиптична орбита с апогей на разстоянието до геостационарната орбита.
• На каква височина над земната повърхност трябва да е перигеят на орбитата на кораба, така че най-кратко време след първата доставка до станцията да бъде направена втората?
• Какво би било това време?
Пояснение: Геостационарна орбита е тази, при която космическата станция обикаля около Земята синхронно с околоосното въртене на нашата планета и остава винаги над една и съща точка от земния екватор.
Справочни данни:
Радиус на геостационарната орбита 42 170 км
Екваториален адиус на Земята 6 370 км
Решение:
Очевидно корабът ще се движи по своята орбита с период, който е по-кратък от този на геостационарната станция. След като веднъж той е направил доставка на станцията, трябва да слезе близо до Земята, за да поеме следващата доставка и после да я отнесе до станцията. Но когато достигне за втори път геостационарната орбита, ще е изминало време, по-малко от орбиталния период на станцията и тя няма да е достигнала точката, в която ще се окаже корабът. Затова той ще продължи по своята орбита надолу и първа възможност за нова доставка ще има при следващото си достигане до геостационарната орбита. Следователно едно от възможните решения е орбиталният период на кораба Т да е точно два пъти по-кратък от този на станцията Т0 . Да означим радиуса на геостационарната орбита с r0 , а голямата полуос на елиптичната орбита на кораба – с r . Съгласно ІІІ закон на Кеплер:
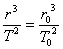
Оттук пресмятаме:

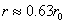
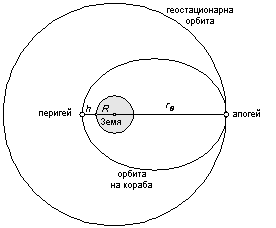
От фигурата виждаме, че височината h на перигея на кораба над земната повърхност може да се изрази по следния начин:
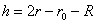
където R е земният радиус.
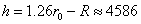 км км
Можем да проверим за други решения на това подусловие, например при период на кораба три пъти по-кратък от този на станцията. Но тогава получаваме, че в апогея си корабът няма да достигне до геостационарната орбита. Същото се отнася в още по-голяма степен за периоди, които са още по-голямо цяло число пъти по-кратки от този на станцията. Следователно двойно по-краткият период е единственото решение. Очевидно времето между две доставки на станцията ще бъде равно на два орбитални периоди на кораба или на един период на станцията, т.е продължителността на едно звездно денонощие – 23ч. 56м.
ПРАКТИЧЕСКИ ТУР
Марс през 2003 година. През 2003 година, по време на поредното велико противостоене, Марс се доближи рекордно близо до нас. На 27 август той беше само на 55758006 километра от Земята. В приложението разполагате с поредица от негативни изображения на Марс, съответстващи на 0h UT (универсално време) за посочените дати. Всички изображения са в еднакъв мащаб. Под датите са дадени и геоцентричните еклиптични дължини на Марс за тези моменти.
• На лист милиметрова хартия начертайте орбитата на Земята в подходящ мащаб. Приемете, че пролетната равноденствена точка се намира наляво, в посока успоредна на милиметровото разграфяване на хартията. Приемайки, че Земята се движи равномерно по кръгова орбита и че противостоенето също е било на 27 август, означете с максимално възможна точност положенията на Марс в съответните моменти от време и нарисувайте участъка от орбитата, по която той се е движил през 2003 година. Приемаме, че орбитите на Земята и Марс лежат в една равнина.
Справочни данни:
1AU (астрономическа единица ) – 150 000 000 km
Продължителност на звездната година – 365d.2564
Решение: Избираме такъв мащаб, че орбитата на Земята върху листа да има радиус 5 сантиметра. Начертаваме я в средата на листа милиметрова хартия. За да определим положенията на Марс, трябва да знаем посоките към планетата и разстоянията до нея. Особеното в случая е това, че наблюдаваме планетата от подвижен обект – Земята. За да може да определим положенията на Марс, трябва да знаем положенията на Земята по нейната орбита в моментите на наблюдение. Като изходно направление за графичните построения избираме посоката към Марс в момента на неговото най-голямо приближаване към Земята, който приехме да съвпада с момента на противостоене. Тогава Слънцето, Марс и Земята лежат на една права линия, която сключва с посоката към пролетната равноденствена точка ъгъл, равен на геоцентричната еклиптична дължина на Марс, измерван против часовниковата стрелка. Този ъгъл е равен на 335.5 градуса. Начертаваме тази линия и означаваме върху орбитата на Земята нейното положение. Разстоянието от Земята до Марс в този момент е rmin= 55758006 км. В мащаба на чертежа разстоянието е:
rMo = ( rmin / 1AU ). 50мм = 18.59 мм
Нанасяме и положението на Марс върху линията.
Нека първо нанесем положенията на Земята върху орбитата и в съответните моменти от време. Пълна обиколка по своята орбита Земята извършва за една звездна година. Следователно за едно денонощие Земята изминава ъгъл равен на:
Δλo = 360/365.2564 = 0°.9856
Виждаме, че наблюденията са правени през 28 денонощия, с изключение на момента на противостоене, който е на 14 денонощия от съседните наблюдения. За 14 дни Земята ще измине ъгъл Δλ1 равен на :
Δλ1 = 14 ×Δλo = 14 ×0°.9856 = 13°.8
По същия начин пресмятаме ъглите Δλ за всеки момент от време. Тези ъгли имат смисъла на разлика в еклиптичната дължина на направлението към Марс, в деня на най-голямото му сближаване със Земята, и еклиптичната дължина в останалите моменти. Тъй като еклиптичната дължина расте в посока съвпадаща с посоката на движението на Земята по орбитата, то ъглите на положенията преди 27 август са положителни, а тези след него – отрицателни. Записваме резултатите в Таблица 1 и нанасяме положенията на Земята по нейната орбита.
За да определим разстоянието от Земята до Марс сравняваме видимите размери на Марс в максималното му приближаване към Земята с размерите му в другите моменти. Разстоянието до Марс е обратно пропорционално на видимия диаметър на изображенията на планетата:
rM / rMo = DMo / DM
Следователно:
rM = (DMo / DM ). rMo
Измерваме диаметрите на изображенията на Марс, за които са дадени моменти от време, и записваме резултатите в Таблица 1. Пресмятаме разстоянията от Земята до Марс върху чертежа в милиметри и също ги записваме в таблицата.
За всяко положение на Земята определяме моментното положение на Марс по дадената геоцентрична еклиптична дължина. Еклиптичните дължини се отчитат от пролетната равноденствена точка и нарастват в посока на движение на планетите и Слънцето по небесната сфера (т.е. против часовниковта стрелка, гледайки от Северния еклиптичен полюс). Центрираме транспортира върху всяко положение на Земята, ориентираме го по милиметровите лини на мрежата, тъй като сме избрали те да са успоредни на направлението към пролетната равноденствена точка. Отбелязваме направлението към Марс и използвайки чертожна линия, нанасяме положението на Марс в това направление на съответното разстояние rM взето от Таблица 1. По този начин нанасяме всички положения на Марс. Построяваме частично орбитата на Марс, прекарвайки през точките плавно огъната линия. Виждаме, че тя описва част от овална фигура – елипса.
Таблица 1. Марс през 2003 година
№ |
Дата |
DM |
rM |
Dl |
|
0h UT |
[мм] |
[мм] |
[ ° ] |
1 |
1.01 |
7.6 |
103.0 |
234.6 |
2 |
29.01 |
8.6 |
91.0 |
207.0 |
3 |
26.02 |
9.9 |
79.0 |
179.4 |
4 |
26.03 |
11.8 |
66.3 |
151.8 |
5 |
23.04 |
14.7 |
53.2 |
124.2 |
6 |
21.05 |
18.4 |
42.5 |
96.6 |
7 |
18.06 |
24.4 |
32.0 |
69.0 |
8 |
16.07 |
32.4 |
24.2 |
41.4 |
9 |
13.08 |
40.6 |
19.3 |
13.8 |
10 |
27.08 |
42.1 |
18.59 |
0.0 |
11 |
10.09 |
40.8 |
19.2 |
- 13.8 |
12 |
8.10 |
32.1 |
24.4 |
- 41.4 |
13 |
5.11 |
24.0 |
32.6 |
- 69.0 |
14 |
3.12 |
18.1 |
43.2 |
- 96.6 |
15 |
31.12 |
14.0 |
55.9 |
- 124.2 |
|
|