|
МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ
ІХ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
http://astro-olymp.org
ІІІ кръг - задачи и решения
Ученици от 7-8 клас
1 задача. Както звнаем от любимата детска книжка, едно от приключенията на Мечо п ух е търсенето и намирането на Северния полюс. Като се е запасил с достатъчно гърнета мед, Мечо Пух е тръгнал да търси Северния полюс на Нова година. След дълго пътешествие по суша и вода, след много дни и нощи, чийто брой той отдавна загубил, най-после навлязал в голяма снежна равнина и решил, че е достигнал целта си. Забил едно колче в намерената от него точка на Северния полюс, но тъй като бил любител-астроном, направил проверка. През интервали от един час отбелязвал с малки колчета положението на края на сянката на голямото колче. При това всеки път измерванията показвали, че дължината на сянката е една и съща.
- Разгледайте рисунката.
- Може ли Мечо Пух да е сигурен, че е открил това, което търси?
- Приблизително по кое време на годината е стигнал до това място?
- Обяснете вашите отговори.
Решение:
Дължината на сянката на колчето, забито от Мечо Пух, наистина не се променя. Това означава, че Слънцето остава на една и съща височина над хоризонта. Така действително би трябвало да е на полюса по време на полярния ден. Само че има и нещо смущаващо. Сянката се върти с течение на времето обратно на часовниковата стрелка. А ако Мечо Пух беше на северния полюс, тя трябваше да се върти по посока на часовниковата стрелка. Следователно той е намерил полюса, но не северния, а южния (виж картинката)! Ъгълът, под който слънчевите лъчи падат спрямо земята, е около 20 градуса и следователно това се е случило недалеч от зимното слънцестоене за нашето северно полукълбо, когато на южния полюс грее Слънце и е полярен ден.
2 задача. Вие сте участници в бъдеща експедиция до Титан – най-големият спътник на Сатурн, обвит в плътна азотна атмосфера. Космическият кораб каца и първото, което виждат космонавтите, е светлият кръгъл диск на Сатурн, прозиращ през метановите облаци. В продължение на 30 земни денонощия членовете на екипажа изследват повърхността на спътника и без прекъсване наблюдават от площадката до кораба Сатурн около зенита – през нощта във видима светлина, през деня в инфрачервена.
- Пресметнете приблизително общото време, през което ще можете да осъществявате радиовръзка със Земята.
- Приемете, че зрителният лъч от Земята лежи в равнината на орбитата на Титан около Сатурн. Сатурн е в опозиция. з а периода на експедицията, орбиталното преместване на планетата, както и движението на Земята, може да пренебрегнете.
Справочни данни:
Орбитален период на движение на Титан около Сатурн – 15.945 денонощия
Радиус на орбитата на Титан около Сатурн – 1 222 000 км
Радиус на Сатурн – 60 268 км
Решение:
Нека отбележим с А мястото на кацане на експедицията. Космонавтите наблюдават от това място Сатурн винаги около зенита.. Следователно орбиталният период на Титан е равен на периода на околоосното му въртене, а оста му е почти перпендикулярна на орбитата му около Сатурн. Така този спътник е винаги обърнат с една и съща страна към планетата, а експедицията е кацнала около центъра на видимия от Сатурн диск на Титан.

Радиовръзката със Земята е възможна в интервалите от време, когато Земята е над хоризонта за мястото на експедицията. Както се вижда от рисунката, това е изпълнено през половината от всеки орбитален период Т на Титан. Но зрителният лъч от Земята лежи в орбиталната равнина на Титан, а Сатурн е в опозиция. Ето защо, през част от това време Титан ще се закрива от Сатурн за земния наблюдател.
Скоростта на движение на Титан по неговата орбита е:
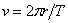
където r е радиусът на орбитата на Титан. Времето, за което Титан е закрит от Сатурн за наблюдател от Земята, е:
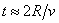
където R е радиусът на Сатурн. Накрая за времето от един орбитален период на Титан, през което радиовръзката със Земята е възможна, получаваме:
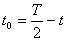
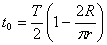
Общият престой на експедицията на Титан е 30 земни денонощия, или малко по-малко от два орбитални периода на спътника. При кацането космонавтите са видели светлия кръгъл диск на Сатурн. Следователно, когато са кацнали там, Сатурн е бил обърнат към спътника с огрятата си от Слънцето страна (положение 1 на фигурата). Местното време е съответствало на средата на нощта за Титан, а също и на средата на неблагоприятния за радиовръзка със Земята интервал. Оттук заключаваме, че за времето около 30 земни денонощия космонавтите са могли да се възползват от два пълни интервала от време t 0 , в които връзката със Земята е била възможна. Общото време за връзка със Земята е било 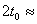 15.444 земни денонощия. 15.444 земни денонощия.
3 задача. Замечтан метеорен наблюдател гледа звездното небе и си мисли за едно желание. Дълго време не може да си го пожелае, защото не се появяват метеори. Вместо тях, при него идва добра вълшебница и му предсказва, че желанието ще се сбъдне. После леко излита нагоре и миг преди да изчезне, пуска облак от милион частици звезден прах. Звездната величина на облака е 3 m . Малко по-късно една прашинка пада в ръката на наблюдателя и от разстояние 30 см свети за него като звездичка от 3-та звездна величина.
На каква височина е изчезнала вълшебницата?
Виж вълшебницата, нарисувана от Десислава Живкова - участничка в олимпиадата.
Справочни данни:
Видимият блясък на един светещ обект е обратно пропорционален на квадрата на разстоянието до него.
Решение:
Щом облакът е от милион (1 000 000) частици, значи на разстояние 30 см от наблюдателя целият облак би имал 1 000 000 пъти по-силен видим блясък, отколкото една своя частица. На височината Н , на която е изчезнала вълшебницата, целият облак е имал същия видим блясък
(3 m ), както една прашинка на разстояние 30 см . Следователно на височината Н облакът е имал видим блясък, 1 000 000 пъти по-слаб, отколкото би имал на разстояние 30 см . Видимият блясък на един светещ обект е обратно пропорционален на квадрата на разстоянието до него. Ето защо височината Н трябва да е 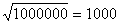 пъти по-голяма от 30 см , или Н = 300 метра . пъти по-голяма от 30 см , или Н = 300 метра .
4 задача. На рисунката виждате диаграма, показваща видимите положения на четирите галилееви спътника на Юпитер – Йо, Европа, Ганимед и Калисто. Като използвате данните от диаграмата, направете подходящи измервания и определете възможно най-точно масата на планетата Юпитер.
Ако сте наблюдавали с телескоп Юпитер в 0 h на днешния ден, как би бил разположен относно планетата всеки един от спътниците? Нарисувайте схема.
Орбиталното движение на Юпитер, както и това на Земята да не се отчита.
Справочни данни:
Съгласно ІІІ закон на Кеплер, ако около космическо тяло с маса М обикаля спътник с много по-малка маса, то 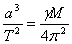 , където а е голямата полуос на орбитата на спътника, Т е неговият орбитален период, а , където а е голямата полуос на орбитата на спътника, Т е неговият орбитален период, а
γ = 6.67×10-11 m3 / kg . s2 е гравитационната константа.
Радиус на Юпитер 71 500 км
Решение:
Определяме мащабите на скалите на диаграмата. По скалата на разстоянията на 80 радиуса на Юпитер отговарят 82 мм. Мащабът е 80/82 » 0.9756 радиуса на Юпитер на милиметър. По скалата на времето на 40 дни отговарят 151 мм. Мащабът е 40/151 » 0.265 денонощия на милиметър.
Измерваме амплитудите на изменение на разстоянията от спътниците до центъра на Юпитер. Това са радиусите на орбитите на спътниците около Юпитер. За по-точни резултати амплитудата на изменение на разстоянието до Юпитер измерваме на няколко места и усредняваме резултатите. Получаваме:
| Спътник |
Радиус на орбитата r00
в мм |
Радиус на орбитата
в радиуси на Юпитер,
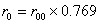 рад.юп./мм рад.юп./мм |
| Йо |
6 |
5.8536 |
| Европа |
9.5 |
9.2682 |
| Ганимед |
15 |
14.634 |
| Калисто |
27 |
26.3412 |
За да определим по-точно орбиталния период на даден спътник, измерваме общата продължителност на колкото е възможно повече периоди върху диаграмата и делим получената стойност на броя периоди. Например за Йо можем да измерим общата продължителност на 21 периода, за Европа – 10, за Ганимед – 5 и за Калисто – 2 периода. Резултатите са следните:
| Спътник |
Орбитален период Т00
в мм |
Орбитален период в денонощия,
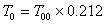 дни/мм дни/мм |
| Йо |
6,68 |
1.7702 |
| Европа |
13,4 |
3.551 |
| Ганимед |
27 |
7.155 |
| Калисто |
62,5 |
16.5625 |
От ІІІ закон на Кеплер:
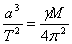
където М е масата на Юпитер, а е радиусът на орбитата на спътника, Т е неговият орбитален период, а γ е гравитационната константа. Масата на Юпитер е:
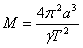
Чрез умножаване по радиуса на Юпитер в километри, превръщаме радиусите на орбитите на спътниците също в километри, а после и в метри. Превръщаме стойностите на орбиталните периоди от денонощия в секунди и заместваме в горната формула. За масата на Юпитер от данните за различните спътници получаваме:
| Спътник |
Маса на Юпитер |
Йо |
1.853×1027 kg |
Европа |
1.828×1027 kg |
Ганимад |
1.773×1027 kg |
Калисто |
1.929×1027 kg |
Окончателно масата на Юпитер получаваме, като средно аритметично на тези резултатите – 1. 846×1027 kg .
Като пресечем диаграмата с хоризонтална линия, съответстваща на 0 h за датата на ІІІ кръг на астрономическата олимпиада (13 май), виждаме, че на този ден спътникът Европа е на изток от Юпитер, а Йо, Ганимед и Калисто са на запад, както е показано на схемата.
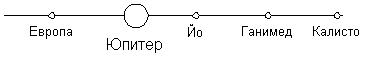
Спътниците разпознаваме по това, че в реда Йо, Европа, Ганимед, Калисто, те са подредени по нарастване на отдалечеността им от Юпитер.
|
|