МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО
И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА
ПО АСТРОНОМИЯ
VІІІ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
http://astro-olymp.org
IІІ кръг - решения
Ученици от 7-8 клас
1 задача.
Както знаете, Малкият принц живее на един от най-малките астероиди в Слънчевата система. Освен Малкия принц, на астероида има три вулкана, една роза и една овца. Овцата не е съвсем обикновена – от едната страна е снежно бяла, а от другата черна. Черната страна на овцата, както и самият астероид, отразява 2% от падналата върху нея светлина. Бялата страна на овцата отразява 96% от светлината. Веднъж, както си стояла на северния полюс на астероида, овцата заспала. Астероидът се върти около оста си, така че овцата се обръща ту с бялата, ту с черната си страна към наблюдателя. Ако площта на “видимия диск” на овцата е 30 пъти по-малка от площта на видимия диск на астероида, с колко звездни величини ще се променя видимият блясък на астероида за земния наблюдател?
Решение:
Бялата страна на овцата отразява 96% / 2% = 48 пъти повече светлина от черната страна. Видимият диск на астероида е 30 пъти по-голям по площ от “видимия диск” на овцата и следователно отразява светлина колкото 30 овце, обърнати към наблюдателя с черната си страна. Когато овцата е обърната към нас с черната си страна, то астероидът с овцата отразява колкото 31 овце. А когато овцата е обърната към нас с бялата си страна, то астероидът с овцата отразява светлина колкото 30 + 48 = 78 овце, обърнати към нас с черната си страна. Във втория случай видимият блясък на астероида ще бъде 78 / 31 ? 2.516 пъти по-силен, отколкото в първия случай. Това означава, че при въртенето на астероида, видимият му блясък се променя с около 1 звездна величина.
2 задача.
 При какви условия можем да видим Луната като лодка над хоризонта на екватора, както е показано на рисунката? Кога през годината може да се случи това? Наклонът на лунната орбита към еклиптиката да не се отчита. Лунната “лодка” е точно хоризонтално уравновесена. При какви условия можем да видим Луната като лодка над хоризонта на екватора, както е показано на рисунката? Кога през годината може да се случи това? Наклонът на лунната орбита към еклиптиката да не се отчита. Лунната “лодка” е точно хоризонтално уравновесена.
Решение:
От рисунката се вижда, че Луната е много тънък сърп. Това означава, че видимото й положение на небето е близо до това на Слънцето, а фазата й е или малко преди новолуние, или малко след новолуние. Малко преди новолуние Луната е на запад от Слънцето. В такъв случай ще я наблюдаваме сутрин преди изгрева на Слънцето в източната част на хоризонта. Малко след новолуние бихме я наблюдавали вечер след залеза на Слънцето в западната част на хоризонта. За да виждаме лунната “лодка”, разположена така, както е на рисунката, линията, свързваща центровете на Слънцето и Луната, трябва да е перпендикулярна на хоризонта. Но тази линия е част от еклиптиката, на която лежат и двете небесни светила. За наблюдател на екватора еклиптиката пресича хоризонта под прав ъгъл при изгрев или пък при залез Слънце в периодите около лятно и зимно слънцестоене. Следователно посоката, в която ще виждаме Луната като лодка сутрин, ще бъде изток-североизток около лятно слънцестоене, или изток-югоизток около зимно слънцестоене.
А посоката, в която ще я виждаме като лодка вечер, ще бъде запад-северозапад около лятно слънцестоене, или запад-югозапад около зимно слънцестоене.
3 задача.
Нарисувайте приблизително на звездната карта еклиптиката. Означете със съответните числени стойности координатните линии за ректасцензията и деклинацията. Нанесете приблизително видимите положения на планетите на днешния ден (5 март 2005 г.). Използвайте данните от таблицата.
Планета |
Меркурий |
Венера |
Марс |
Юпитер |
Сатурн |
α |
23 h 58 m |
2 2 h 41 m |
19 h 21 m |
1 3 h 05 m |
7 h 29 m |
δ |
0?12' |
– 10?15' |
– 23?47' |
– 5?17' |
21?57' |
Кои от планетите биха се виждали в нощта на 5-ти срещу 6-ти март и кои – не?
Решение:
Очевидно в центъра на картата е северният небесен полюс. (Виж фигурата) Концентричните кръгове около него са паралелите, а радиално разположените прави линии са деклинационните кръгове (небесните меридиани). Те са 12 на брой, което означава, че са прекарани през 2 h по ректасцензия. Като знаем, че небесният екватор минава през пояса на Орион, определяме и кой от паралелите съответства на него. От екватора до небесния полюс разстоянието е 90?. Оттук следва, че паралелите са прекарани през 30?.
Намираме съзвездието Риби. Близо до дясната “риба” (западно от квадрата на Пегас) се намира пролетната равнодествена точка ^ . Точното й положение е пресечната точка на съответния най-близък деклинационен кръг с екватора. Този деклинационен кръг съответства на ректасцензия 0 h . От него се ориентираме, за да нанесем ректасцензята и на другите деклинационни кръгове през 2 h , имайки предвид, че тя нараства по посока на годишното движение на Слънцето по еклиптиката. За тази посока можем да се ориентираме по реда на следване на зодиакалните съзвездия. Пресечната точка на диаметрално противоположния деклинационен кръг с екватора е есенната равноденствена точка d . Точките ^ и d са двете пресечни точки на еклиптиката с небесния екватор. Точките на лятно и зимно слънцестоене определяме като лежащи на меридианите с ректасцензии съответно 6 h и 18 h , и отстоящи на около 23.5? над екватора и под екватора. После очертаваме приблизително еклиптиката.
Накрая, след като имаме координатна мрежа с числени означения и като използваме данните от таблицата, нанасяме полаженията на планетите. Датата 5 март е с около 16 дни, или половин месец по-рано от пролетното равноденствие, когато Слънцето е в точката ^ . Следователно на 5 март Слънцето е на около 1 h по ректасцензия преди (или западно) от ^ , т.е. между планетите Венера и Меркурий. Самите две планети са на около 20? една от друга. Това означава, че те са много близо до Слънцето и ще се губят в неговите лъчи. Венера и Меркурий не могат да се наблюдават в нощта на 5/6 март 2005 г. Всички останали планети – Марс, Юпитер и Сатурн са на големи ъглови разстояния от Слънцето и могат да се наблюдават в различни моменти от същата нощ.
4 задача.
На 10 октомври 2004 г. Луната е в съединение с Венера. На 12 октомври същата година. Луната е в съединение с Юпитер. На 28 октомври има лунно затъмнение. А на 4 ноември има съединение на Венера с Юпитер. Нарисувайте приблизително как са били разположени по своите орбити Венера, Юпитер и Земята на 4 ноември 2004 г. Обяснете вашето решение.
Решение:
Тъй като на 10 октомври има съединение на Луната с Венера (положение 1 на фигурата).а само два дни по-късно – съединение на Луната с Юпитер (положение 2), то Юпитер е на изток от Венера. Луната изминава около 13? на денонощие на фона на звездите, затова ъгловото разстояние между Венера и Юпитер е между 13? и 26?. Посочваме тези граници, понеже не знаем точно моментите на съединенията. На 28 октомври има лунно затъмнение, което означава, че тогава Луната е в пълнолуние (положение 3). Това е 16 дни след съединението на Луната с Юпитер. Следователно при съединението на Луната с Юпитер фазата на Луната е била около два дни преди новолуние и тя трябва да е била на малък ъгъл западно от Слънцето (положение 2). Оттук заключаваме, че и Юпитер е на малко ъглово отстояние западно от Слънцето. Юпитер се движи твърде бавно по своята орбита и за интервала от време между 12 октомври и 4 ноември неговото преместване е незначително. Затова при решаването на тази задача го приемаме за неподвижен. Орбиталният период на Венера е около 8 месеца. За периода от 10-12 октомври до 4 ноември тя се е придвижила от положение 1 приблизително до положение 4. От 28 октомри до 4 ноември Земята се е отместила малко по своята орбита и от новата й позиция се наблюдава съединение на Венера с Юпитер.

5 задача.
Два спътника се движат по кръгови орбити в равнината на земния екватор. Единият се движи в посоката на въртенето на Земята, а другият в обратна посока. В даден момент от време за един наблюдател на земния екватор двата спътника минават едновременно през зенита. След три часа спътниците отново преминават едновременно през зенита на същия наблюдател, и така на всеки три часа.
Какви са орбиталните периоди на двата спътника? Кой от спътниците е на по-висока орбита? Каква е разликата във височините на двата спътника?
Ако спътникът, двиежещ се в обратна посока, е на височината на геостационарната орбита, през какъв интервал от време ще се случват срещите на спътниците в зенита на наблюдателя? Какъв е периодът на спътника, който се движи в правата посока? Стигнете до отговора само посредством разсъждения, без формули и дълги пресмятания.
Справочни данни :
Маса на Земята 5.98 ? 10 24 kg
Гравитационна константа 6.67 ? 10 -11 m 3 / kg . s 2
Звездно денонощие 23 h 56 m 04 s Решение:
Нека преминаванията през зенита стават в моменти, означени на фигурата с 1 и 2. Земята се върти на изток, затова спътникът, който се движи в права посока, трябва да обиколи веднъж Земята и после допълнително да измине дъгата от орбитата си от точка 1 до точка 2. Спътникът, движещ се в обратна посока, ше стигне до зенита в точка 2 преди да е затворил една обиколка. Следователно спътникът на по-ниска орбита трябва да се движи в права посока, а спътникът на по-висока орбита – в обратна посока.
Нека Т 0 е интервалът от време между две преминавания през зенита, Т е времето, за което Земята прави една обиколка около оста си, Т 1 е времето, за което първият спътник (движещ се в права посока) прави една обиколка около Земята, Т 2 е времето, за което вторият спътник (движещ се в обратна посока) прави една обиколка около Земята.
 Тъй като интервалът от време между две преминавания на спътник през зенита е неговият синодичен период за земния наблюдател, за двата спътника можем да напишем уравненията: Тъй като интервалът от време между две преминавания на спътник през зенита е неговият синодичен период за земния наблюдател, за двата спътника можем да напишем уравненията:
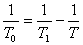 ? ? 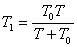
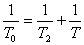 ? ? 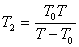
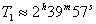
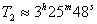
Използваме ІІІ закон на Кеплер в обобщен вид за двата спътника:
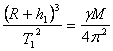 ? ? 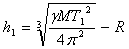
където R е радиусът на Земята, а h 1 e височината на първия спътник. Аналогично за височината на втория спътник получаваме:
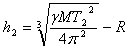
За разликата във височините получаваме:
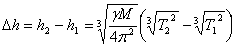 = 1 786.3 km = 1 786.3 km
Спътник на геостационарна орбита, но движещ се в обратна посока, ще преминава през зенита за неподвижен наблюдател през 12 звездни часа, т.е. 11 h 58 m 02 s средно слънчево време, защото спътникът и Земята имат еднаква ъглова скорост, но се въртят в противоположни посоки. Тъй като и първият спътник трябва да е в зенита на наблюдателя в същия момент, той трябва да направи за 12 звездни часа една и половина обиколки около Земята. Следователно той прави една обиколка за 8 звездни часа, което е 7 h 58 m 41.4 s средно слънчево време.
|