|
МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО
И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА
ПО АСТРОНОМИЯ
VІІІ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
http://astro-olymp.org
ІV кръг - решения
Ученици младша възраст (до 15 г.)
1 задача. За младия астроном Жельо Желев, от всички космически обекти, принадлежащи към Слънчевата система, най-интересни са метеорните тела. Той си задава въпроса колко бърз може да е най-бързият метеор. Максималната скорост, с която е възможно метеорно тяло да навлезе в земната атмосфера, е около 72 км/сек.
• Обяснете защо е така.
• Пресметнете максималната видима ъглова скорост, която може да има един метеор за земния наблюдател. Приемете, че метеорът се появява на височина 100 км от земната повърхност.
• При какви условия (кога и къде) може да се види такъв метеор?
• Най-ентусиазираните наблюдатели мечтаят да видят метеор с ъглова скорост, по-голяма от изчислената. Какво би могло да се каже за такъв метеор?
Решение: Едно метеорно тяло би имало максимална линейна скорост относно Земята, ако в момента на срещата му с нашата планета са изпълнени следните условия:
1) Тялото се движи относно Слънцето с максималната възможна скорост. На разстояние от Слънцето, равно на радиуса r на земната орбита, това е параболичната скорост:
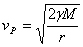 » 42 km/sec » 42 km/sec
където М е масата на Слънцето.
2) Тялото трябва да се движи в посока обратна на орбиталното движение на Земята, което се извършва със скорост v3 » 30 km/sec . При това скоростта на метеорното тяло относно Земята е
vM = vP + v3 » 72 km/sec .
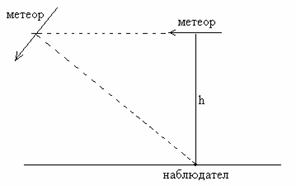 За да бъде максимална видимата ъглова скорост на метеора, той трябва да е в зенита за наблюдателя. В противен случай метеорът би се появил на по-далечно линейно разстояние от наблюдателя и ъгловата му скорост би била по-малка. Метеорът трябва да е ориентиран успоредно на земната повърхност, т.е. радиантът му трябва да е на хоризонта. Иначе наблюдателят би виждал проекция на метеора и съответно по-малка ъглова скорост. За За да бъде максимална видимата ъглова скорост на метеора, той трябва да е в зенита за наблюдателя. В противен случай метеорът би се появил на по-далечно линейно разстояние от наблюдателя и ъгловата му скорост би била по-малка. Метеорът трябва да е ориентиран успоредно на земната повърхност, т.е. радиантът му трябва да е на хоризонта. Иначе наблюдателят би виждал проекция на метеора и съответно по-малка ъглова скорост. За 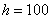 km височина видимата ъглова скорост на метеора би била km височина видимата ъглова скорост на метеора би била
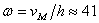 °/sec . °/sec .
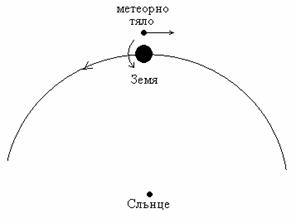 Най-бърз метеор би се видял в полунощ над екватора. Тогава към неговата скорост би се добавила и линейната скорост на въртене на екваториална точка от земната повърхност. Времето от годината трябва да е около преминаването на Земята през перихелия, защото тогава и орбиталната скорост на Земята, и параболичната скорост за едно метеорно тяло относно Слънцето са по-големи. Най-бърз метеор би се видял в полунощ над екватора. Тогава към неговата скорост би се добавила и линейната скорост на въртене на екваториална точка от земната повърхност. Времето от годината трябва да е около преминаването на Земята през перихелия, защото тогава и орбиталната скорост на Земята, и параболичната скорост за едно метеорно тяло относно Слънцето са по-големи.
Ако наблюдаваме по-бърз метеор от този, то бихме направили извода, че той се предизвиква от метеорно тяло, което не принадлежи на Слънчевата система, а идва от междузвездното пространство и се движи относно Слънцето по хипербола със скорост по-голяма от параболичната скорост.
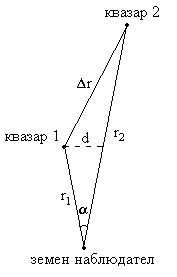
2 задача. В две галактики са разположени квазари, чието ъглово разстояние един от друг е 1". Масата на едната галактика се оказва пренебрежимо малка спрямо другата. Червеното преместване на техните спектри е съответно
z1 = 0.436 и z2 = 0.437.
• Определете при каква минимална маса те биха могли да бъдат гравитационно свързани помежду си. При решаването на задачата считайте стойността на константата на Хъбъл Н = 75 ( km/sec )/Mpc .
Решение: От величините на червеното преместване за двата квазара можем да намерим скоростите, с които те се отдалечават от нас:
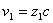 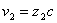
където с е скоростта на светлината. Съгласно закона на Хъбъл за разширението на Вселената, разстоянията до двата квазара са съответно:
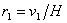 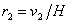
 където Н е константата на Хъбъл. където Н е константата на Хъбъл.
Разликата между двете разстояния е:
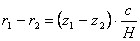
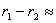 4 Mpc 4 Mpc
На разстоянието от нас до първия квазар 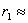 1744 Mpc ъгловото отстояние между двата квазара 1744 Mpc ъгловото отстояние между двата квазара 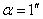 съответства на линейно разстояние: съответства на линейно разстояние: 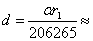 0.0085 Mpc, което е много по-малко от 0.0085 Mpc, което е много по-малко от 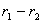 . Следователно можем да считаме, че . Следователно можем да считаме, че 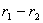 е приблизително равно на разстоянието между двата квазара е приблизително равно на разстоянието между двата квазара 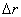 . Също така можем да считаме, че относителната скорост на единия квазар спрямо другия има компонента по зрителния лъч от земния наблюдател: . Също така можем да считаме, че относителната скорост на единия квазар спрямо другия има компонента по зрителния лъч от земния наблюдател:
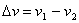
Тъй като нямаме информация за компонентата на относителната скорост, перпендикулярна на зрителния лъч, ние не знаем каква е пълната относителна скорост на единия квазар спрямо другия. Единствено можем да кажем, че пълната скорост е не по-малка от 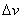 . Засега приемаме, че . Засега приемаме, че 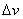 е пълната скорост. Тогава, за да бъдат двете галактики гравитационно свързана система, тази скорост трябва да е по-малка от скоростта на избягване на разстоянието между двата квазара. Ако по-масивната галактика има маса М (масата на другата е много по-малка), то можем да напишем: е пълната скорост. Тогава, за да бъдат двете галактики гравитационно свързана система, тази скорост трябва да е по-малка от скоростта на избягване на разстоянието между двата квазара. Ако по-масивната галактика има маса М (масата на другата е много по-малка), то можем да напишем:
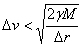
Оттук следва:
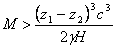
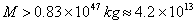 слънчеви маси слънчеви маси
Предвид това, че изчисленията не бяха направени с истинската пълна относителна скорост, минималната маса, която търсим, може да се окаже и по-голяма от получената стойност.
3 задача. Участници в астрономическата олимпиада тръгват от Стара Загора на експедиция с хелиев балон. Кацат на непознато място и се опитват да определят координатите си. Наблюдават звездата γ Касиопея
(α = 0h53m40s, δ = +60°27') в горна кулминация на 17°51'25" от зенита. Моментът на кулминацията, отчетен от Игнат, е 0h53m50s. Старата черна врана, която са взели за консултант, мъдро им припомня, че часовникът им върви по местното звездно време на Старозагорската обсерватория (λ = 1h42m32s, φ = 42°25'35"). Какви са координатите на непознатото място? Опишете приблизително пейзажа, който участниците виждат около себе си.
Решение: Трябва да разгледаме два случая.
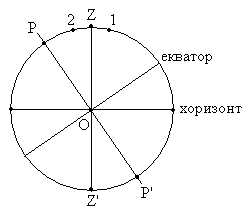 1) Звездата кулминира на разстояние 1) Звездата кулминира на разстояние 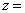 17°51'25" южно от зенита (точка 1 на фигурата). Тогава географската ширина на мястото е 17°51'25" южно от зенита (точка 1 на фигурата). Тогава географската ширина на мястото е
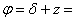 78°18'25" северна ширина. За да намерим географската дължина, използваме факта, че моментът по местно звездно време на горната кулминация на една звезда е равен на ректасцензията на звездата. В случая местното звездно време трябва да е: 78°18'25" северна ширина. За да намерим географската дължина, използваме факта, че моментът по местно звездно време на горната кулминация на една звезда е равен на ректасцензията на звездата. В случая местното звездно време трябва да е:
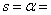 0h53m40s 0h53m40s
Виждаме, че то е с 10 секунди назад от показанието на часовника (0h53m50s), което е по местното звездно време в Стара Загора. Следователно мястото, където е кацнал балонът, е на 10 секунди западно от Стара Загора и географската дължина на това място е λ = 1h42m22s.
Като имаме предвид високата северна ширина, то пейзажът, който ще виждат около себе си участниците в експедицията, ще бъде ледове и снегове.
2) Звездата кулминира северно от зенита (точка 2 на фигурата). Географската дължина на мястото ще бъде същата. Географската ширина ще бъде
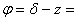 42°35'35&. Това е само с 10' северно от град Стара Загора по ширина и 10 секунди западно по дължина. Като знаем, че една дъгова минута по земната повърхност отговаря на една миля, или около 1.85 км, можем да пресметнем, че мястото ще бъде на около 18.5 км северно и на около 3.4 км западно от Стара Загора. Пейзажът ще бъде хълмове, покрити с гори, и села. (По-точно, това е близо до знаменитото за олимпийската лагер-школа през 2005 г. село Змейово). 42°35'35&. Това е само с 10' северно от град Стара Загора по ширина и 10 секунди западно по дължина. Като знаем, че една дъгова минута по земната повърхност отговаря на една миля, или около 1.85 км, можем да пресметнем, че мястото ще бъде на около 18.5 км северно и на около 3.4 км западно от Стара Загора. Пейзажът ще бъде хълмове, покрити с гори, и села. (По-точно, това е близо до знаменитото за олимпийската лагер-школа през 2005 г. село Змейово).
4 задача. В приложената таблица са дадени звездните величини на една променлива звезда за определени моменти от време (в денонощия), отчетени от произволно начало.
• Постройте кривата на блясъка на звездата. Определете от нея моментите на максимум на звездата, като използвате метода на хордите.
• Пресметнете периода на звездата.
• Определете амплитудата на промяна на блясъка.
• От какъв тип е променливата звезда?
Време, d |
Звездна величина |
Време, d |
Звездна величина |
- 0.01 |
7.48 |
0,38 |
7,76 |
0.01 |
7.36 |
0,44 |
7,77 |
0,03 |
7,28 |
0,49 |
7,78 |
0,06 |
7,28 |
0,53 |
7,72 |
0,09 |
7,36 |
0,55 |
7,64 |
0,12 |
7,42 |
0,56 |
7,49 |
0,17 |
7,52 |
0,58 |
7,36 |
0,21 |
7,60 |
0,60 |
7,28 |
0,26 |
7,68 |
0,62 |
7,28 |
0,34 |
7,74 |
0,66 |
7,36 |
|
|
0,71 |
7,47 |
Решение: Нанасяме точките. Прекарваме плавна крива през тях. Построяваме по няколко хорди близо до максимумите, успоредни на времевата ос. Намираме и отбелязваме средите на хордите. През тях прекарваме прави линии до пресичането им с кривата на блясъка в областта на максимумите. Точките на пресичане са точките на максимумите върху кривата на блясъка. Отчитаме по времевата ос координатите на точките и това са моментите на максимумите. От момента на по-късния максимум изваждаме момента на по-ранния и получаваме периода. По оста на звездните величини отчитаме стойностите в максимум и минимум и от разликата им получаваме амплитудата на звездата.
T1max= 0d.04 T2max= 0d.61 P = T1max- T2max= 0d.57
m1max= 7m.27 m2max= 7m.27 mcp max= 7m.27
mmin= 7m.78
Амплитудата е A = mmin - mmax= 0m.51.
Кривата на блясъка е цефеидоподобна,  , но периодът е само 0d.57. Следователно променливата звезда е от типа RR Lyr . , но периодът е само 0d.57. Следователно променливата звезда е от типа RR Lyr .

Крива на блясъка на променливата звезда
Справочни данни :
Маса на Слънцето M = 2 ? 1030 kg
Гравитационна константа γ = 6.67 ? 10-11 m3/kg.sec2
|
|