МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО
И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА
ПО АСТРОНОМИЯ
ІХ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
http://astro-olymp.org
ІV кръг - решения
Ученици младша възраст (до 15 г.)
1 задача. Ярка мъглявина с видим размер 1° представлява остатък от взрив на свръхнова, който е станал преди 10 000 години. През мъглявината се виждат добре по-далечни обекти, а в нейния спектър присъства ярка широка линия на водорода Нα. Линията се простира в област от дължини на вълните от 6541 до 6585 ангстрьома. Мъглявината се осветява от намиращата се съвсем наблизо много гореща звезда от спектрален клас О, чиито видим блясък е 3m.
Оценете линейния размер на мъглявината.
Оценете светимостта на горещата звезда в единици светимост на Слънцето.
Какво може да се каже за радиуса на звездата в сравнение с радиуса на Слънцето?
Справочни данни:
Абсолютна звездна величина на Слънцето 4m.76
Решение: Размиването на водородната линия в спектъра на мъглявината се дължи на продължаващото разширение на мъглявината след избухването на звездата. Тъй като през мъглявината се виждат по-далечни обекти, то тя е достатъчно прозрачна. Това означава, че към нас идва светлина от целия обем на мъглявината. Приемаме, че поради разширението на мъглявината, веществото от най-предната – най-близката до нас нейна част се приближава към нас със скорост v относно центъра й, а веществото от най-далечната част на мъглявината се отдалечава от нас със скорост –v . Ефектът на Доплер води до разширение на спектралната линия в област от λ1= 6541 Å до λ2 = 6585 Å. Скоростта v намираме от съотношението:
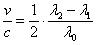
където с е скоростта на светлината, а 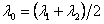 е дължината на вълната, съответстваща на средата на интервала, в който се простира спектралната линия, или на светлината, идваща от централната част на мъглявината. Така получаваме: е дължината на вълната, съответстваща на средата на интервала, в който се простира спектралната линия, или на светлината, идваща от централната част на мъглявината. Така получаваме:
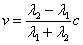
Щом взривът на свръхновата е станал преди време
t = 10 000 години, то можем да оценим нейния линеен размер:
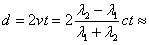 0.0067 с ×10000 г.= 67 светлинни години ≈ 20 pc 0.0067 с ×10000 г.= 67 светлинни години ≈ 20 pc
Видимият ъглов размер на мъглявината е α= 1°. Чрез него пресмятаме и разстоянието до нея:
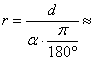 3800 св. г. ≈ 1100 pc 3800 св. г. ≈ 1100 pc
Тъй като горещата звезда от звездна величина m = 3m е в съседство с мъглявината, ще смятаме, че и тя е на същото разстояние от нас. Абсолютната звездна величина на звездата М намраме от съотношението:

Като сравним с абсолютната звездна величина на Слънцето MS = 4m.76 , за светимостта на звездата L в единици светимост на Слънцето LS получаваме:
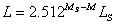
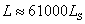
Ако означим с R и RS радиусите на звездата и на Слънцето, а с T и TS – техните температури, то можем да напишем:
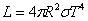

където σ е константата на Стефан-Болцман. Разделяме почленно двете равенства:
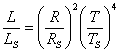
За отношението на радиусите на звездата и Слънцето е:
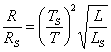
Температурата на горешите звезди от спектрален клас О е около 50 000 К, а на Слънцето около 6000 К. За радиусите получаваме:
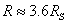
2 задача. Вие сте светлозелени жители на Алфа, живеещи в съдружие с вашите виолетови съседи от Бета под лъчите на светилото Гама. Можете да виждате Бета само от едната страна на Алфа. Вашето алфа-денонощие съдържа 16 бета-цикъла. Всеки от тях е равен на времето между две преминавания на Блестящия бета-остров през централния меридиан на видимия диск на Бета. А времето между две обръщания на северната полярна бета-шапка към вас е равно на 15 бета-цикъла.
От гледна точка на жителите на Бета, колко бета-денонощия съдържа една година (една обиколка около Гама)?
Решение: От условието на задачата става ясно, че системата Алфа – Бета представлява двойна планета, или система от спътник и планета, обикалящи около звздата Гама. Бета се вижда само от едната страна на Алфа, което значи, че Алфа е винаги обърната с една и съща страна към Бета. Следователно периодът Ta* на околоосно въртене на Алфа е равен на периода, с който тя обикаля около Бета. Той се равнява на периода между две обръщания на северната полярна бета-шапка към Алфа, или на 15 бета-цикъла. Но това е сидеричният период на околоосно въртене на Алфа. А денонощието на Алфа, или нейният синодичен период Ta на околоосно въртене спрямо светилото Гама, е 16 бета-цикъла. Той е по-дълъг от Ta*, което означава, че околоосното въртене на Алфа става в същата посока, както обикалянето на системата Алфа-Бета около звездата Гама. Периода на орбитално движение на системата около Гама, или продължителността на годината Ta, можем да намерим от равенството:
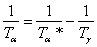
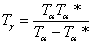
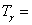 16 × 15 = 240 бета-цикъла 16 × 15 = 240 бета-цикъла
Годината, или времето за обиколка на системата Алфа-Бета около звездата Гама, съдържа 15 слънчеви алфа-денонощия по 16 бета-цикъла, или 16 звездни алфа-денонощия по 15 бета-цикъла.
В един сидеричен период Ta* на обикаляне на Алфа около Бета (времето между две обръщания на северната полярна бета-шапка към Алфа) има 15 бета-периода. Това е броят на завъртанията на Бета около нейната ос за един сидеричен период на обикаляне на Алфа около Бета. Но това са околоосните завъртания на Бета за наблюдател от Алфа. Относно неподвижните звезди броят на околоосните завъртания на Бета ше бъде с 1 по-голям, т.е. 16. Годината Тγ съдържа 16 сидерични или звездни алфа-периода. Следователно общият брой на звездните бета-денонощия в годината е 16 алфа-периода в една година ×16 завъртания на Бета в един алфа-период = 256. Това са звездните бета-денонощия в една година. Слънчевите бета-денонощия в годината ще бъдат с 1 по-малко от звездните. Ето защо, за жителите на Бета в годината има 255 денонощия.
3 задача. През лятото на 2026 г. астрономът Калоян Генков извършва наблюдения от борда на геостационарна космическа станция. В свободното си време той дава консултации по GSM на участниците в астрономическия лагер “The Dishes” в източната част на Африка с координати φ= 0°, λ= 45°. В помощ на обучението, Калоян решава да изпрати контейнер с научна информация и част от своите хранителни запаси до лагера.
Отговорете само качествено с каква скорост и в каква посока трябва да се изхвърли контейнерът от станцията, така че да пада вертикално към Земята.
Направете оценка за координатите на астрономическата обсерватория, над която се намира станцията. Приблизително в коя част на света е тя?
Влиянието на атмосферата да не се отчита.
Справочни данни:
Радиусът на геостационарната орбита е приблизително 7 пъти по-голям от радиуса на Земята.
Решение: Геостационарният спътник се движи в екваториалната равнина на Земята по посока на нейното околоосно въртене с период Т , равен на едно звездно денонощие, или 23 h 56 m . Радиуса на орбитата му означаваме с r . За да пада контейнерът вертикално към Земята, той трябва да се изхвърли от спътника в посока, обратна на неговото движение, със скорост, равна по големина на скоростта на спътника.
За да оценим времето за падането на контейнера на Земята, предполагаме, че той се движи по много силно сплесната елиптична орбита около центъра на нашата планета с голяма полуос, равна на половината от радиуса на геостационарната орбита. Периодът на движение на спътника по такава орбита Т1 можем да намерим с помощта на III закон на Кеплер:
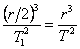
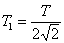
Времето за падането на контейнера ще бъде половината от този период, или:
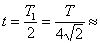 4 h 14 m 4 h 14 m
Но това е времето, за което контейнерът би паднал не до земната повърхност, а до центъра на Земята. Радиусът на Земята обаче, е само около 1/7 от радиуса на орбитата на спътника. Освен това за изминаването на тази последна 1/7 от пътя си до центъра на Земята, в случай, че цялата й маса беше съсредоточена в една точка там, контейнерът би изразходвал много малко време в сравнение с останалата част от пътуването си, защото би се движил с много голяма скорост. Ето защо можем да пренебрегнем това и да считаме, че времето за падане на контейнера на земната повърхност е приблизително 4 часа. За тези 4 часа Земята ще се завърти на около 4×15° = 60° на изток. Ето защо точката на падането на контейнера ще бъде на 60° западно от обсерваторията, над която „виси” геостационарният спътник. Географските координати на обсерваторията ще бъдат φ = 0°, λ = 105°. Това е някъде в Индонезия.
Практическа задача. Двойнствеността на спектрално двойните звезди се установява чрез спектрални наблюдения. В таблицата са дадени данни за лъчевите скорости на компонентите на спектрално двойната звездна система p от Корабни платна .
Изследвайки кривата на лъчевите скорости, покажете приблизително как са ориентирани орбитите на компонентите й спрямо наблюдател на Земята, като приемете, че зрителният лъч лежи в орбиталната равнина. Изчислете отношението на масите на двете компоненти.
No |
T |
V1
km/s |
V2
km/s |
1 |
0 d 00.0 h |
23.1 |
13.2 |
2 |
0 d 14.4 h |
6.6 |
39.6 |
3 |
0 d 20.5 h |
1.2 |
52.8 |
4 |
1 d 06.8 h |
-19.8 |
85.8 |
5 |
1 d 11.9 h |
-39.6 |
98.7 |
6 |
1 d 19.5 h |
-46.2 |
92.4 |
7 |
1 d 23.2 h |
-36.3 |
72.6 |
8 |
2 d 07.4 h |
-4.9 |
42.9 |
9 |
2 d 15.6 h |
9.9 |
33.1 |
10 |
3 d 01.8 h |
16.5 |
23.2 |
11 |
3 d 18.6 h |
26.4 |
8.2 |
12 |
4 d 18.8 h |
36.3 |
-3.3 |
13 |
5 d 21.5 h |
39.6 |
-6.6 |
14 |
6 d 20.1 h |
37.9 |
-9.9 |
15 |
8 d 04.8 h |
36.3 |
-3.3 |
16 |
9 d 09.5 h |
26.4 |
8.2 |
17 |
9 d 19.8 h |
23.1 |
13.2 |
18 |
10 d 06.1 h |
14.9 |
23.1 |
19 |
10 d 15.2 h |
3.3 |
36.3 |
20 |
11 d 02.5 h |
-19.8 |
62.7 |
Решение: Построяваме кривите на изменеие на лъчевите скорости на двете компоненти на системата. Виждаме, че на високия остър пик на лъчевата скорост на компонентата 1 съответства дълбок стръмен спад на лъчевата скорост на компонентата 2. На полегатия плавен спад на лъчевата скорост на звездата 1 съответства полегато плавно увеличение при звездата 2. Това се дължи на факта, че около моментите на минимумите и максимумите на лъчевите скорости направлението на действителните скорости на звездите е близко до направлението на зрителния лъч от земния наблюдател. Освен това, острите пикове и спадове отразяват бързото и силно нарастване на радиалната компонента на скоростта на всяка от звездите около перицентъра на нейната орбита относно центъра на масите на системата. Полегатите пикове и спадове отразяват движението на компонентите около апоцентровете на техните орбити. Симетричността на пиковете и спадовете говори за това, че всъщност скоростите на звездите в самите перицентрове и в апоцентровете на техните орбити практически съвпадат по направление със зрителния лъч. Следователно големите оси на елиптичните орбити на звездите са разположени перпендикулярно на зрителния лъч от земния наблюдател. Зрителният лъч лежи в равнината на орбитите. Следователно лъчевите скорости в перицентровете и апоцентровете на елиптичнита орбити на звездите, измерени по върховите стойности на графиката, са равни на действителните скорости на звездите в тези точки.
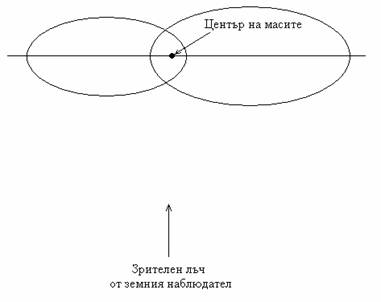
Прекарваме хоризонтална линия през точките, където двете графики на лъчевите скорости се пресичат. Нивото на тази линия определя лъчевата скорост, с която се движи центърът на масите на двойната звездна система относно нас. Тя е vС = 20 км/с. Когато определяме лъчевата скорост на коя да е от звездите в даден момент чрез измерване и отчитане по графиката, от тази измерена стойност винаги вадим vС , за да получим лъчевата скорост на звездата относно центъра на масите.
Означаваме с vp1 , va1 , vp2 , va2 скоростите в перицентъра и в апоцентъра съответно на зведата 1 и на звездата 2. От измерванията, като приведем стойностите към движение относно центъра на масите на системата, получаваме:
vp1 = 80 км/с
va1 = 30 км/с
vp2 = 65 км/с
va2 = 20 км/с
Отношението на масите на двете звезди М1 и М2 е:
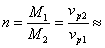 0.8 0.8
|