|
МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО
И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА
ПО АСТРОНОМИЯ
ХI НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
http://astro-olymp.org
ІV кръг, практически тур - решения
Ученици младша възраст (до 16 г.)
Задача 1. Морско пътешествие.
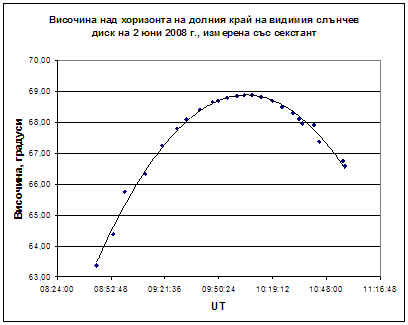
След дълго пътешествие из далечни страни и морета кръжочниците по астрономия към варненската обсерватория Сашо и Мишо тръгват към родния бряг. На борда на своята яхта те всеки ден определят координатите си. За целта измерват височината на долния край на видимия слънчев диск със секстант, а край тях се разхожда пъстроцветният тукан, който са намерили в Никарагуа. В таблицата са представени измерванията, направени от смелите мореплаватели на 2 юни 2008 г. Определете техните координати в този ден. Според вас, в кое море са се намирали тогава? Видимият ъглов радиус на Слънцето на 2 юни 2008 г. е 15°48´.
UT |
Височина |
UT |
Височина |
° |
|
° |
08:45:00 |
63,36 |
10:35:00 |
67,95 |
08:54:00 |
64,38 |
10:41:00 |
67,92 |
09:00:00 |
65,75 |
10:44:00 |
67,38 |
09:11:00 |
66,34 |
10:57:00 |
66,75 |
09:20:00 |
67,25 |
10:58:00 |
66,60 |
09:28:00 |
67,80 |
09:33:00 |
68,10 |
10:08:00 |
68,88 |
09:40:00 |
68,40 |
10:13:00 |
68,81 |
09:47:00 |
68,65 |
10:19:00 |
68,70 |
09:50:00 |
68,70 |
10:24:00 |
68,50 |
09:55:00 |
68,80 |
10:30:00 |
68,32 |
10:00:00 |
68,85 |
10:33:00 |
68,12 |
10:04:00 |
68,88 |
Решение:
Начертаваме графика, представяща изменеието на височината на Слънцето с времето. Прекарваме плавна крива през получените точки. От нея определяме максималната височина, на която се издига долният край на видимия слънчв диск. Тя е 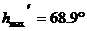 . Ако . Ако  е видимият ъглов радиус на Слънцето, то максималната височина на неговия център над хоризонта е е видимият ъглов радиус на Слънцето, то максималната височина на неговия център над хоризонта е 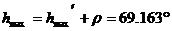 . Тогава географската ширина на яхтата ще бъде . Тогава географската ширина на яхтата ще бъде 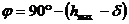 ,
където δ е деклинацията на Слънцето. От дадената ни страница за юни 2008 г. в Астрономическия алманах виждаме, че деклинацията на Слънцето в 0h UT на 2 юни е била 22°12´, а на 3 юни е била 22°20´. От графиката установяваме, че Слънцето е било в горна кулминация около 10h UT на 2 юни. Чрез интерполиране намираме деклинацията му за този момент: ,
където δ е деклинацията на Слънцето. От дадената ни страница за юни 2008 г. в Астрономическия алманах виждаме, че деклинацията на Слънцето в 0h UT на 2 юни е била 22°12´, а на 3 юни е била 22°20´. От графиката установяваме, че Слънцето е било в горна кулминация около 10h UT на 2 юни. Чрез интерполиране намираме деклинацията му за този момент:

Така получаваме:
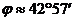
Географската дължина можем да намерим, като определим точния момент, в коъто Слънцето е било в горна кулминация. Това правим чрез графиката, като използваме метода на хордите. Начертаваме върху получената от нас крива поредица от хорди и определяме техните среди. Прекарваме права линия през тези средни точки и определяме точката, в която тя пресича кривата. Тази точка съответства на търсения от нас момент. Поради симетричността на кривата, начертаната от нас права линия през средните точки на хордите е перпендикулярна на оста на времето. По точката, в която тя пресича оста на времето определяме момента на горна кулминация на Слънцето. Той е 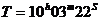 UT. Моментът на горна кулминация на Слънцето трябва да е в UT. Моментът на горна кулминация на Слънцето трябва да е в  по местно време. Сравнявайки двата момента, можем да пресметнем географската дължина: по местно време. Сравнявайки двата момента, можем да пресметнем географската дължина:
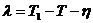
където ? е уравнението на времето, равно на средното слънчево време минус истинското. От дадената диграма на уравнението на времето намираме, обаче, че за 2 юни то е приблизително равно на 0. Окончателно за географската дължина получаваме:
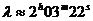
Определените от нас координати на яхтата показват, че мореплавателите Сашо и Мишо са вече доста близо до България и се намират в родното Черно море.
Задача 2. Наблюдение на окултация на звезда от астероид.
Десет наблюдатели, разположени както е показано на схемата, наблюдават окултация на звездата TYC 1065-021222-1 от астероида 225 Хенриета на 16 юни 2007 г. Звездата има координати 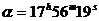 и и 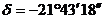 . Нейната звездна величина е 11.67m, а на астероида 12.46m. Хоризонталният денонощен паралакс на астероида, гледан от Земята, е 5.56" . Астероидът има ъглово преместване на фона на звездите m =24,84"/h. . Нейната звездна величина е 11.67m, а на астероида 12.46m. Хоризонталният денонощен паралакс на астероида, гледан от Земята, е 5.56" . Астероидът има ъглово преместване на фона на звездите m =24,84"/h.
Някои от наблюдателите са наблюдавали само едно закриване на звездата, а други, поради неправилната форма на астероида, две закривания. За всички тях той се намира близо до зенита. В таблицата са дадени моментите на закриване и откриване на звездата за всеки наблюдател.
Считайте, че видимият размер на астероида е много по-голям от този на звездата (откриването и закриването са мигновенни).
А) Начертайте посоката на движение на сянката на астероида и обяснете зависи ли тя от конфигурацията между Земята и него.
Б) Опитайте се да възстановите профила и размерите на астероида.
В) Намерете орбиталния период на астероида, като приемете, че той се движи по кръгова орбита.
Не отчитайте околоосното въртенето на астероида по време на окултацията.
Екваториален радиус на Земята – 6378 km
Решение:
А) Датата на окултацията е 17 юни, т.е. съвсем близо до лятното слънцестоене. От друга страна координатите на звездата, респективно и на астероида, сътоветстват на положение около точката зимното слънцестоене. Можем да направим извода, че астероидът се намира много близо до опозиция. Понеже астероидът е на орбита с по-голям радиус от орбиталния радиус на Земята, то неговата скорост е по-малка от земната. Следователно, Земята „изпреварва” сянката му. Това означава, че по земната повърхност сянката се движи от изток на запад, или в посока обратна на посоката на движение на Земята по орбитата й. Начертаваме тази посока върху схемата.
Посоката на движение на сянката зависи от конфигурацията на астероида и Земята. Когато позицията на астероида е близка до някоя от квадратурите например, цялата орбитална скорост на Земята е насочена към него. Тогава планетата ни не се движи спрямо сянката на астероида и относителното движение на сянката по земната повърхност е в посока на орбиталното движение на астероида. То е в същата посока като движението и на Земята – от запад на изток.
Б) Първо привеждаме общите съображения, въз основа на които работим. Звездата се намира много далеч от нас и затова считаме, че идващият от нея светлинен сноп е успореден. Следователно, сянката (областта от която се вижда окултацията на звездата) има контур, отговарящ на профила на астероида. С течение на времето тази сянка се придвижва по земната повърхност и различни наблюдатели могат да наблюдават окултацията. През всеки наблюдател преминава една хорда от този контур с определена дължина l.
За времето на окултацията t сянкатата очевидно изминава път l по траекторията си. Нейната скорост е равна на тангенциалната компонента на скоростта на астероида относно Земята Vτ. Тя може да бъде изразена като произведение на ъгловото преместване за единица време μ и разстоянието r от Земята да астероида. Разстоянието пресмятаме, използвайки дадения ни денонощен паралакс p и радиуса на Земята R . Така получаваме:
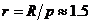 АU АU
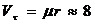 км/с км/с
След като за време t астероидът се премества на разстояние l, то 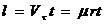 . Оттук следва, че всеки наблюдател, като измерва продължителността на покритието, може да пресметне дължината на преминалата през него хорда. Спрямо всички наблюдатели сянката се движи в една и съща посока, т.е. през тях преминават успоредни една на друга хорди от профила. Използвайки горната формула, получаваме за хордите, преминали през всички наблюдатели: . Оттук следва, че всеки наблюдател, като измерва продължителността на покритието, може да пресметне дължината на преминалата през него хорда. Спрямо всички наблюдатели сянката се движи в една и съща посока, т.е. през тях преминават успоредни една на друга хорди от профила. Използвайки горната формула, получаваме за хордите, преминали през всички наблюдатели:
Наблюдател |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Дължина [km] |
80 |
41 |
38 |
78 |
14 |
27 |
76 |
36 |
25 |
77 |
Дължина [km] |
|
44 |
38 |
|
|
25 |
|
33 |
|
|
За наблюдателите, които са наблюдавали две покрития, интервалите от време между края на първото и началото на второто са :
Наблюдател |
2 |
3 |
6 |
8 |
Интервал [s] |
3,1 |
2,4 |
6,9 |
5,5 |
Следователно разстоянията между края на първото покриване и началото на второто са:
Наблюдател |
2 |
3 |
6 |
8 |
Разстояние [km] |
25 |
19 |
55 |
44 |
За да получим профила е необходимо да нанесем хордите в еднакъв мащаб в един и същи момент от време. За мащаб избираме 1 см = 20 км. Начертаваме ос Ох по посока на движението на сянката. За всеки наблюдател нанасяме съответната хорда така, че началото й да лежи в точката на наблюдателя, успоредно на Ох. За тези, които са наблюдавали две закривания, чертаем и двете хорди с прекъсването между тях. След като сме изпълнили тази процедура, остава да намерим положението на всички хорди в един и същи момент от време, например началото на окултацията за наблюдател 1. За тази цел правим следното. Намираме времената между началото на окултацията за първия и всички останали наблюдатели. Техните стойности са:
Наблюдател |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Интервал [s] |
30,4 |
27,8 |
35,1 |
34,8 |
40,4 |
51,2 |
51,4 |
27,8 |
15,7 |
Ако за даден наблюдател интервалът е Dt, то за него хордата трябва да се премести на разстояние 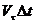 в посока обратна на движението на сянката, тъй като през наблюдател 1 тя е минала първо. Оттук получаваме, че разстоянията, на които трябва да се транслират хордите, са: в посока обратна на движението на сянката, тъй като през наблюдател 1 тя е минала първо. Оттук получаваме, че разстоянията, на които трябва да се транслират хордите, са:
Наблюдател |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Дължина [km] |
241 |
220 |
279 |
274 |
321 |
407 |
408 |
220 |
125 |
Дължина [cm] |
4,8 |
4,4 |
5,6 |
5,5 |
6,4 |
8,1 |
8,2 |
4,4 |
2,5 |
Сега вече имаме положенията на хордите в момента, в който започва окултацията за наблюдател 1. За да получим окончателно профила, свързваме краищата на хордите. Понеже астероидът е близо до зенита, то не се налага да разглеждаме деформация поради проекцията на сянката върху сферата. Получава се контур на заек. От мащаба на хордите намираме, че дебелината на астероида е между 80 и 120 км.
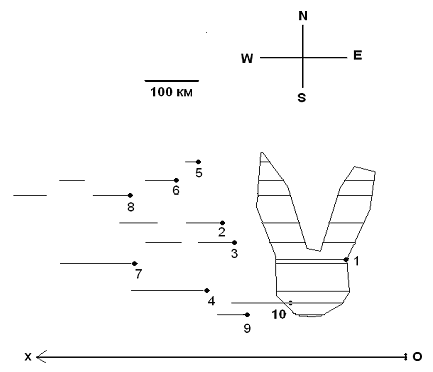
В) Получихме, че разстояните до астероида е r = 1.5 AU. Понеже той е в опозиция, радиусът на неговата орбита е a = 1.5 + 1 = 2.5 AU. От третия закон на Кеплер за търсения период Т имаме,
a[AU]3 / T[год.]2 = 1,
откъдето пресмятаме Т ≈ 1,8 год.
Ученици старша възраст (до 18 г.)
Задача 1. Вълни на Мортън в атмосферата на Слънцето
Дадени са три негативни изображения на част от слънчевия диск, получени през 3 минути. В резултат на слънчевото избухване, по повърхността на Слънцето тръгва вълна, която може да се види на второто и третото изображение. В горния десен край на изображенията са дадени моментите от време, в които те са били получени.
Очертайте фронта на вълната на изображенията и пресметнете средната скорост, с която вълната се е движила между тези два момента (на второто и третото изображение).
Слънчевото избухване е станало в слънчево петно, което се вижда на негативните изображения като малко светло петънце в левия край на голямо факелно поле ( тъмното петно). Ако слънчевото избухване е станало в 18:43:59 UT, каква е била средната скорост на вълната в първите две минути? Дали вълната ще успее да обиколи цялата слънчева повърхност?
Сравнете скоростта на вълната с втора космическа скорост за Слънцето. Как ще коментирате резултата?
Радиус на Слъцето – 700000км.
Маса на Слънцето – 2.1030 кг.
Решение:
Очаква се вълната да има сферична симетрия, но понеже явлението се наблюдава в края на диска, виждаме фронта на вълната като елипса. Очертаваме фронта на двете изображения. Построяваме една хорда на слънчевия диск и нейната симетрала. Очевидно симетралата ще бъде диаметър на диска. Определяме центъра на слънчевия диск като средата на тази симетрала. За хордата и нейната симетрала прилагаме правилото на пресичащите се хорди:
ab = cd
където a и b са дължините на отсечките, на които е разделена едната хорда при пресичането си с другата хорда, а c и d са отсечките, на които се делидругата. Оттук определяме диаметъра на слънчевия диск. Същото можем да направим и използвайки две хорди и пресечната точка на техните симетрали.
Свързваме центъра на избухването с центъра на слънчевия диск с права линия и пренасяме успоредно тази права на второто и третото изображение. Измерваме разстоянието от центъра на слънчевия диск до слънчевото петно и до точките на пресичане с фронта на вълната върху второто и третото изображение.
Да построим разрез на Слънцето през слънчевото петно и центъра на слънчевия диск. Нека S е положението на слънчевото петно върху повърхността на Слъцето, а F1 и F2 са положенията на фронта на вълната в двата момента от време върху слънчевата повърхност. Нека OA = ao е разстоянието от центъра на диска на Слънцето до слънчевото петно, OB = a1 и OC = a2 са разстоянията от центъра на диска на Слънцето до фронта на вълната в двата момента, измерени по правата, свързваща центъра на слънчевия диск и слънчевото петно, в което се е случило слъчевото избухване.
За да намерим средната скорост v23, с която вълната се разпространява между второто и третото изображение, трябва да измерим разстоянието, което тя изминава по слънчевата повърхност. На нашия чертеж това е дъгата l, имаща централен ъгъл 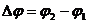 . От чертежа се вижда, че . От чертежа се вижда, че 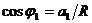 и и 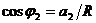 , където R е радиусът на Слънцето, измерен върху изображението с намерения център на слънчевия диск. От тези съотношения намираме ъглите φ1 , φ2 и Δφ. , където R е радиусът на Слънцето, измерен върху изображението с намерения център на слънчевия диск. От тези съотношения намираме ъглите φ1 , φ2 и Δφ.
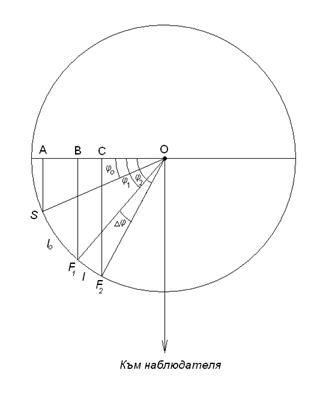
Дължината на дъгата l по повърхността на Слънцето в километри е
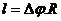
Тогава
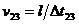
където Δt23 е интервалът от време между моментите на второто и третото изображение.
По подобен начин намираме дължината на дъгата l0 и средната скорост v12 на разпространение на вълната от момента на слънчевото избухване до момента, запечатан на изображение 2.
От измерванията получаваме:
R = 93.5 mm, a0 = 83 mm, a1 = 52 mm, a2 = 38 mm.
За l получаваме:
l = 120000 km
и скорост
v23 = 665 km/s.
За l0 получаваме:
l0 = 352000 km
и скорост
v12 = 2860 km/s
Виждаме, че вълната много бързо забавя своето движение и най-вероятно ще изчезне преди да успее да обиколи Слънцето.
Използвайки дадената маса на Слънцето М, пресмятаме втора космическа скорост за него. Получаваме 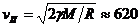 km/s (γ е гравитационната константа). Виждаме, че в първите минути вълната се разпространява със скорост по-голяма от скоростта на избягване от Слънцето. Въпреки това тук няма противоречие защото в действителност получените скорости са скорости на разпространение на вълнов процес, при което не се пренася вещество, а само енергия. km/s (γ е гравитационната константа). Виждаме, че в първите минути вълната се разпространява със скорост по-голяма от скоростта на избягване от Слънцето. Въпреки това тук няма противоречие защото в действителност получените скорости са скорости на разпространение на вълнов процес, при което не се пренася вещество, а само енергия.
Задача 2. Същата като задача 2 за младша възраст.
|
|