МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО
И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА
ПО АСТРОНОМИЯ
ХIІ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
http://astro-olymp.org
ІV кръг, практически тур - решения
Ученици младша възраст (до 16 г.)
Задача. В таблицата са представени данни от измервания на видимия ъглов диаметър на Луната през опреден период от 2009 г. Начертайте графика на изменението на видимия ъглов диаметър с времето. По графиката определете кога Луната е в перигея и в апогея на своята орбита.
Пресметнете ексцентрицитета на лунната орбита.
Определете разстоянието от Земята до Луната в перигей и апогей. Радиусът на Луната е 1737.1 км.
Решение:
Начертаваме графиката на изменението на видимия ъглов диаметър на Луната с времето. Прекарваме плавна крива през точките. По метода на хордите определяме моментите, когато Луната е в перигей – най-близо до Земята и следователно с най-голям видим ъглов диаметър, и в апогей – с най-малък ъглов диаметър. За да определим момента на перихелия, намираме средите на хоризонталните хорди, свързващи възходящата част на графиката до точка Ар и низходящата част. Прекарваме права линия през тези хорди. Точката Ар е пресечната точка на графиката с тази права. Спускаме перпедникуляр от Ар до скалата на времето. Намираме времевата координата на тази точка чрез интерполация. Измерваме отсечките х1 и d . Както виждаме по скалата, отсечката d отговаря на интервал от 5 денонощия. Момента на перихелия намираме по интреполационната формула:
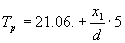 денонощия денонощия
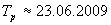 , 03 h UT , 03 h UT
Чрез интерполация по вертикалната ос намираме, че когато Луната е в перигей, нейният видим ъглов диаметър е 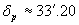 . По аналогичен начин получаваме за момента на апогея . . По аналогичен начин получаваме за момента на апогея .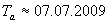 , 01 h UT и видим ъглов диаметър на Луната , 01 h UT и видим ъглов диаметър на Луната 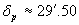 . .
Перицентралното и апоцентралното разстояние при движение по елипса около някакъв гравитационен център са свързани с ексцентрицитета е на орбитата чрез следните формули:
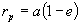
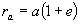
къдета а е голямата полуос на елипсата. Разделяме почленно двете уравнения и получаваме:
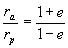
Но ние знаем, че:
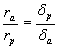
Оттук пресмятаме:
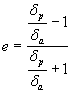
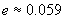
Разстоянието до Луната в перигей намираме от съотношението:
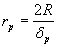
където R е радиусът на Луната в километри, а dp е нейният видим ъглов диаметър в радиани.
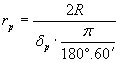
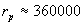 км км
Аналогично за разстоянието в апогей получаваме
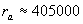 км. км.
Ученици старша възраст (до 18 г.)
Задача. С цел по-точно определяне на константата на Хъбъл космическият телескоп Хъбъл е предприел наблюдение на цефеиди в 18 галактики. Една от тези галактики е М100, намираща се в големия куп от галактики в Дева. Разполагате с криви на блясъка на 8 цефеиди (серии А, В) в галактиката М100. Използвайки таблицата с данни за цефеиди в нашата галактика, определете разстоянието до М100.
Цефеиди в Млечния път |
|
|
|
|
№ |
Абс. зв. |
Период Р |
lg P |
|
величина |
дни |
|
1 |
-2,86 |
3,728 |
|
2 |
-3,66 |
7,024 |
|
3 |
-4,73 |
16,386 |
|
4 |
-5,16 |
23,013 |
|
5 |
-5,81 |
38,768 |
|
6 |
-6,16 |
51,063 |
|
Забележка: Абсолютните звездни величини са средни звездни величини, определени от кривите на блясъка на галактическите цефеиди.

Галактиката М100
Построяваме графично зависимостта период-светимост, като по абсцисата нанасяме логаритъма от периода, а по ординатата абсолютната звездна величина, така че блясъкът да нараства нагоре. По дадените криви на блясъка на цефеиди в М100 определяме техните периоди и средните им звездни величини. Тъй като те се намират практически на едно и също разстояние от нас, за тях също можем да посторим подобна зависимост, която всъщност ще бъде зависимост видима звездна величина – логаритъм от периода. Диаграмата построяваме в същия мащаб по двете оси както и диаграмата за галактическите цефеиди, но върху прозрачна милиметрова хартия. Налагаме диаграмата за М100 върху диаграмата за галактическите цефеиди, така че стойностите по абсцисите им да съвпадат. Придвижваме вертикално нагоре или надолу диаграмата за М100 докато графиката на зависимостта период – звездна величина на М100 съвпадне с графиката за галактическите цефеиди. По ординатната ос отчитаме разликата в звездни величини на двете графики. Използваме формулата за връзката между видимата, абсолютната звездна величина (m и M) и разстоянието r :
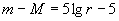
Разликата в звездните величини се получава 31.2m и за разстоянието намираме:
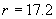 Mpc Mpc
|