МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА

ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА ПО АСТРОНОМИЯ

ХIV НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ

http://astro-olymp.org

  Ученици младша възраст (до 16 г.)

1 задача. Разстояние до галактиката NGC 6822.
Червените гиганти са звезди, които се характеризират с инертно хелиево ядро и слой „горящ” водород около него. С течение на времето тяхната светимост постепенно нараства. Когато светимостта им достигне точно определена стойност, която ще наричаме критична, ядрото се запалва отново и в него започват  реакции на горене на хелия. Това води до рязка промяна в параметрите на тези звезди.
След изчерпване на хелия в ядрото, те са вече с променен строеж и химичен състав и част от тях стават по-ярки от критичната, за обикновените червени гиганти, светимост. Този стадий от звездната еволюция се нарича Асимптотичен Клон на Гигантите (AGB). Звездите преминават през него за по-кратък интервал от време и затова те са значително по-малобройни.
Червените гиганти и AGB звездите са толкова ярки, че могат лесно да бъдат наблюдавани в близки галактики. В  Таблица 1  е даден броят на звездите наблюдавани в галактиката NGC 6822 (галактика джудже в Местната група) в различни интервали от звездни величини.
• Постройте графика, показваща броя звезди в зависимост от интервала звездни величини. Тази графика се нарича „Функция на светимост”.
• Определете звездната величина, при която се включват хелиевите реакции за червените гиганти в NGC 6822.
•Като използвате информацията в  Таблица 2, опитайте да определите разстоянието до тази галактика.
• В  Таблица 2  е дадена видимата звездна величина, при която се включват хелиевите реакции за 4 други галактики в местната група и техните модули на разстоянието. Представете вашия отговор в килопарсеци.

Таблица 1

Таблица 2

Решение. Построяваме функцията на светимостта за галактиката NGC 6822. Тя изглежда по следния начин:

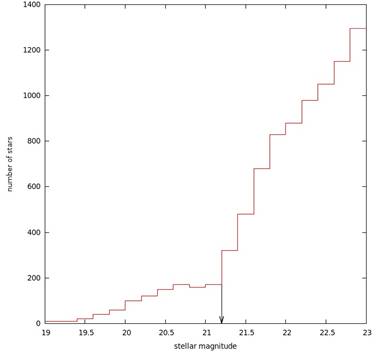
Забелязваме, че при звездна величина около 21.2 има рязък скок в броя на звездите. Именно това е критичната звездна величина, при която започват хелиевите реакции в ядрата на червените гиганти. По-ярките и малобройни звезди са от Асимптотичния клон на гигантите.
В условието е казано, че хелиевите реакции се включват, когато звездите достигнат точно определена светимост. Следователно, можем да използваме тази стойност, за да определим разстоянието до галактиката.
Като използваме информацията от Таблица 2, калибрираме връзката между звездната величина и модула на разстоянието. Прекарваме през точките линейна зависимост и нанасяме върху правата измерената критична звездна величина за галактиката NGC 6822. Това е показано на следната фигура:

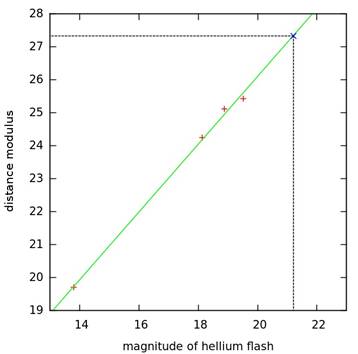
От графиката виждаме, че модулът на разстоянието до  NGC 6822 e 27.3 зв. в.
Използваме формулата за абсолютна звездна величина, за да намерим разстоянието в парсеци:

M = m + 5 – 5 lg r [pc]
m–M = 5 lg r - 5
lgr = (m-M+5)/5
r = 3000 kpc

Критерии за оценяване:
За построяване функцията на светимоост: 4 т.
За определяне критичната зв. в.: 4 т.
За построяване на калибровъчната крива: 3 т.
За опредляне на модула на разстоянието: 2 т.
За изчисляване на разстоянието: 3 т.

Задача 2. Околоосно въртене на Юпитер.
Разполагате с поредица от снимки на Юпитер, направени на 14 август 2009 г. Направете необходимите измервания върху облачните образувания в атмосферата на Юпитер, означени с A, B и C, за да определите периода на околосно въртене на всяко от тях. Определете също така и техните „юпитерографски” ширини.
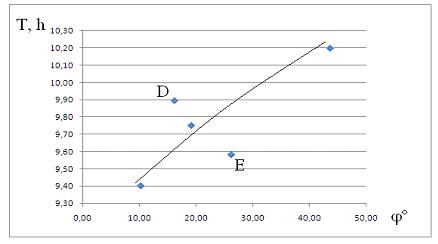
• Постройте графика, показваща зависимостта на периода на въртене на облачните образувания от местоположението им по ширина.
• Определете периодите на движение около оста на Юпитер и за образуванията D и E, както и техните ширини. Нанесете данните за тях на същата графика.

При построяването на графиката вземете ширините само по абсолютни стойности, независимо от това, че някои от облачните петна са в северното, а други в южното полукълбо на Юпитер.
• Какво можете да кажете за посоката, в която се върти около собствената си ос атмосферният вихър, наречен Голямото червено петно?

Обяснете вашите отговори.

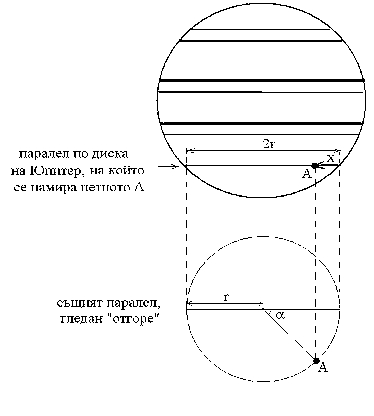
Упътване: За да определите ъгъла, на който се е завъртяло дадено облачно петно около оста на Юпитер, можете да използвате графичен метод. Разгледайте пояснителния чертеж. (По аналогичен начин можете да определите и ширината на петното.)    

Решение:
За всяко от петната измерваме разстоянието х от дясната граница на видимия диск на Юпитер, както е показано на схемата. Петното лежи на определен паралел от „повърхността” на Юпитер с радиус r . Този паралел се проектира върху видимия диск на Юпитер като хорда с дължина 2r. Измерваме и тази дължина. Начертаваме изглед „отгоре” на паралела – окръжност с радиус r , и по проекцията на облачното образувание възстановяваме истинското му положение върху паралела. С транспортир измерваме ъгъла α. Без да правим тези построения, можем да пресметнем ъгъла и по формулата  α = arccos (r-x / r). По същия начин върху кръга нанасяме истинските положения на облачното петно и в други моменти от време. Така виждаме как се изменя ъгълът a  с времето. Нека в два момента от време t₁  и  t₂  облачното образувание да е имало положения, съответстващи на ъгли a₁  и  a₂ . Тогава периода  Т  на въртене на това петно около оста на Юпитер намираме чрез следната пропорция:
T / (t₂ – t₁) = 360° / (a₂ –a₁)
T = 360° (t₂ – t₁) / (a₂ –a₁)
Можем да вземем двете крайни положения на петното – в момента, когато то за първи път се появява на някое от изображенията, и в момента, когато се вижда за последен път. За още по-голяма точност е добре да определим периода по няколко различни положения на петното и да усредним получените стойности. Така процедираме и с другите посочени петна.
Ширината, на която се намира дадено петно, определяме като начертаем диаметър на едно от изображенията, съответстващ на екватора на Юпитер. После правим построенията, показани на фигурата вляво, и измерваме ъгъла φ  –  ширината на петното.

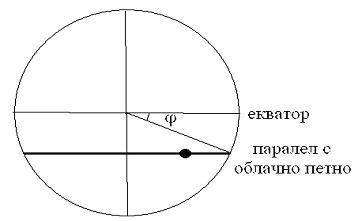
Този ъгъл можем да намерим и по формулата:

 φ= arccos (d / D) ,

където d  и D  са съответно диаметърът на паралела с петното и диаметърът на екватора на Юпитер, измерени по изображението.
Накрая получаваме следните резултати:

По тези резултати построяваме графика на зависимостта на периода на въртене на петната от тяхната ширина. На нея виждаме, че Юпитер не се върти като твърдо тяло. Облачните и газови маси в неговата атмосфера имат различни периоди на въртене, които плавно нарастват с увеличаване на ширината. Най-бързо се вътят зоните около екватора. Но петната D и E се отклоняват от общата тенденция на изменение на периода на околоосно въртене. Петното D има по-дълъг период от образуванията на същата ширина на Юпитер и сякаш изостава от тях, а петното Е, напротив, избързва. Забелязваме, че тези две петна са много близо до Голямото червено петно на Юпитер. То представлява огромен атмосферен вихър, който очевидно влияе на движенията на газовете и облаците около него. От отклоненията в скоростите на петната D и E правим заключението, че вихърът в Голямото червено петно се върти в посока обратна на часовниковата стрелка.

Знаем, че Голямото червено петно е в южното полукълбо на Юпитер. Както е известно от земната метеорология, в южното полукълбо обратно на часовниковата стрелка се въртят вихрите около центровете на високо налягане, или антициклоните. Следователно Голямото червено петно на Юпитер е един огромен антициклон – център на повишено налягане. Също както и при земните антициклони, такива центрове на Юпитер съответстват на локално разясняване на времето. Така че Голямото червено петно е една пролука в облаците на Юпитер, през която можем да наблюдаваме по-дълбоки слоеве от неговата атмосфера.

Критерии за оценяване:
За правилен теоретичен подход при определяне на позициите на петната по ъглова дължина върху диска на Юпитер – графичен или тригонометричен – 2 т.
За правилни измервания и определяния на периода на всяко от петната и верни числени резултати – общо 2.5 т.
За подобряване на точността на периодите чрез усредняване по повече от две позиции на всяко петно – 2.5 т.
За определяне на ширините на петната – 2.5 т.
За правилно построяване на графиката – 2 т.
За добро оформление на графиката с обозначаване на осите, величините и мерните единици – 1.5 т.
За разсъждения относно посоката на въртене на Голямото червено петно – 2 т.
За правилно определяне на посоката на въртене на този вихър – 1 т.

Ученици старша възраст (до 18 г.)

Задача 1:  
Разполагате със снимка на метеор от метеорния поток Персеиди, получена при наблюдателна експедиция на място с координати  λ =37° и.д.   φ=55° с.ш.. Снимката е направена с камера, пред която се е намира двувитлов обтюратор (електромотор с перка, която през определени интервали от време засенчва обектива на камерата) с период на въртене 900 оборота в минута. Към края на метеорната следа се забелязва неголямо избухване на метеора. Това избухване е видяно от друг наблюдател, който се е намирал на 3км на север от камерата. Той забелязва, че избухването е точно върху звездата Вега, която в този момент е в горната си кулминация.
Определете височината на метеора над земната повърхност в момента на избухването и средната скорост на метеора в атмосферата на Земята.
Ъгловото разстояние между Вега и радианта на метеорния поток Персеиди в момента на наблюдение е 74°.  Използвайте приложента карта на съзвездието Лира.

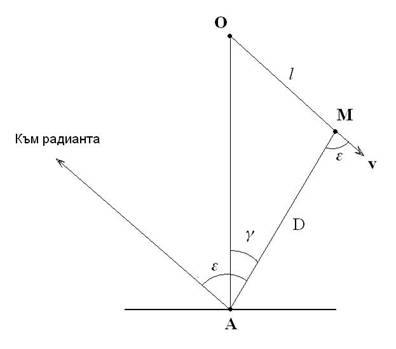
Решение:  Нека първо определим височината на метеора. Да означим мястото на наблюдение като точка А, мястото от което е видяно съвпадащото с Вега избухване на метеора – като точка В.  Точката на избухване на метеора означаваме с М .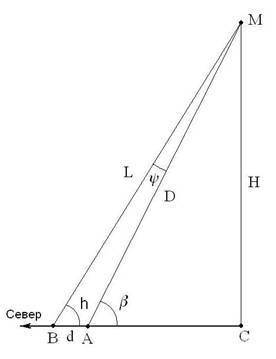

За географска ширина  φ = 55°  Вега кулминира на юг от зенита.  Построяваме схема на разположението на двамата наблюдатели и точката на избухване на метеора – М. Когато наблюдателят от по-северната точка В вижда избухването на метеора, Вега е в горна кулминация. Тъй като наблюдателят в точка А  се намира на същия меридиан, то и за него Вега е в горна кулминация. За да намерим паралактичното отместване на метеора относно двамата наблюдатели, трябва да определим ъгъла, на който се е преместил метеорът (избухването на метеора) за първия наблюдател. Това е ъгловото отстояние на избухването на метеора от изображението на Вега.

За целта първо определяме ъгловото разстояние на две или повече звезди, които се виждат както на снимката, така и на картата на съзвездието Лира. Примерно избираме звездата  γ Лира и най-горната звезда на картата, с която разполагаме. Те са на приблизително еднаква ректасценция  и е удобно да използваме разликата в деклинациите им, за да определим мащаба на снимката. За снимката получаваме мащаб приблизително  0.172°/мм .  Определяме ъгловото разстояние между избухването на метеора и Вега. В горна кулминация Вега се движи по направление от изток на запад, което е перпендикулярно на паралактичното отместване на метеора. Затова от точката на избухване спускаме към трека на Венера перпендикуляр и по него мерим ъгловото разстояние. Получаваме, че за първия наблюдател избухването е отместено на ъгъл y=2°.24, относно втория наблюдател. Приемаме, че височината на Вега е еднаква за двамата наблюдатели. Разстояние от три километра дава само една и половина дъгови минути разлика в географските ширини. За височината на избухването на метеора може да запишем:

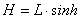
От синусовата теорема следва:

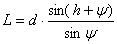
[sin(180°–(h+y)) = sin(h+y)]

Следователно:

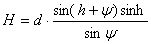
Височината  h  на Вега над хоризонта намираме от географската ширина на мястото на наблюдение и деклинацията на звездата, която определяме от приложената карта. За деклинацията на Вега получаваме: d≈39° . Намираме височината на Вега над хоризонта:

h = 90° – φ + δ = 74° .

Накрая пресмятаме и получаваме за височината на метеора:    H = 72km
Разстоянието до метеора от т.А получаваме от правоъгълния триъгълник ACM и от определената височина H:

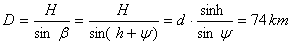
За да получим средната скорост на метеора, първо измерваме ъгловата му дължина  γ , като използваме получения мащаб за снимката. При измерването на дължината се стремим да отчетем и най-слабите следи оставени от метеора. Линейната му дължина върху снимката е около 193 мм, а ъгловата е  γ = 33°.   Възстановяваме щрихите в началото на следата, където границата им не се вижда ясно. Накрая преброяваме около 33 щриха в цялата следа на метеора.
Пространствената дължина на метеора получаваме като отново използваме синусовата  теорема (Фиг.2).

За наблюдателя в т.А, където се намира камерата с обтюратора, крайната точка на метеорната следа е на около 2° от следата на звездата Вега. Следователно ъгловото отстояние на края на следата от радианта на Персеиди е  ε = 72°.

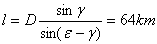
Съществен момент в получаване на решението е това, че пространствената скорост на  метеора е успоредна на направлението към радианта, гледано  от земния наблюдател.
Скоростта на обтюратора е 900 оборота в минута. Това са 15 оборота в секунда. Има две витла които в рамките на един оборот затъмняват обектива на камерата. Следователно прекъсванията са през 1/30 от секундата. Тъй като изображението има 33 щриха, то продължителността на метеора е Δt = 1.1s. Остана да получим средната скорост на метеора:

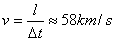
Критерии за оценяване:
За правилни разсъждения и принципна постановка на задачата, при определяне на височината на метеора, както и за правилно определяне на мащабите на снимката – 4т.
За правилна математическа постановка на задачата и за пресмятане на височината – 4т.
За правилна принципна постановка на задачата при определянето на дължината на метеорната следа – 3т.
За правилни измервания, разсъждения и определяне на средната ъглова скорост на метеора – 3т.
За правилни разсъждения и определяне на средната пространствена скорост на метеора – 2т. 

Задача 2. Собствено движение на звезда
На поредица от фотографии, направени от космическия телескоп “Хъбъл” в продължение на една година, е заснета една и съща област от небето, намираща се в съзвездието Дракон. Една от звездите на снимките се е оказала на сравнително малко разстояние от Земята, което позволява да се наблюдава нейното по-бързо преместване спрямо остналите звезди.
Според измерванията на астрономите, нейната хелиоцентрична лъчева скорост е равна на   +20 км/сек. Установено е, че тя е звезда, която няма спътници.
Използвайки фотографиите, намерете тази звезда, определете разстоянието до нея и пространствената й скорост спрямо Слънцето.
Имайки предвид всички получени при решението на задачата данни, какво още бихте казали за тази звезда?

Решение:
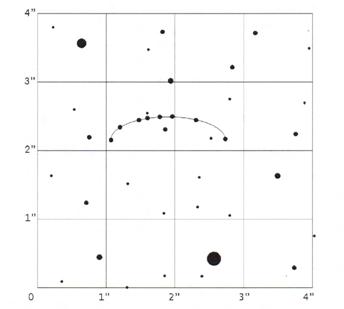
Посредством нанасяния върху паусна хартия се определя последователността от отделните положения на звездата, получени в различни наблюдателни моменти в продължение на една година. През това време звездата е описала кръг по небесната сфера за сметка на паралактичното й движение (нека припомним, че тя се намира в съзвездието Дракон, близо до северния еклиптичен полюс). Кръгът обаче, се е превърнал в разтеглена дъга, тъй като върху паралактичното преместване на звездата се е наложило нейното собствено движение в западна посока, което е равно на 1,6″. Можем да определим амплитудата на преместване на звездата в посока перпендикулярна на собственото движение (около 0,35″). Това е удвоената стойност на годишния паралакс на звездата. Използвайки тези данни и формулата  D = a/sin π,  където  a  е голямата полуос на орбитата на Земята, а π – годишният паралакс на звездата, чрез допълнителни пресмятания можем да получим разстоянието до звездата  D, равно на 6 парсека.
След всичко това, можем да изчислим тангенциалната скорост на звездата  v_t , равна на  1,6″ / 0,35″ ≈ 9 а. е./год. или 43 км/сек. Като знаем лъчевата скорост v_r , пространствената скорост на звездата можем да получим от уравнението  v = ( v_r² + v_t²)^1/2 ≈ 47 км/сек.
Фотографската звездна величина на звездата определяме, използвайки фотографските стандарти, представени графично в горната част на схемата. Можем да преценем, че блясъкът на звездата е равен на 17^m. Оттук можем да определим стойността на абсолютната звездна величина по формулата: M = m + 5 - 5lgr , където r е разстоянието до звездата. Получаваме за нея M =  18^m .
Имайки предвид получените данни за разстоянието и светлинните характеристики на звездата, можем да кажем, че тя е много слаба звезда – джудже.

Критерии за оценяване:
За откриване на звездата на фотографиите и отразяването на нейното годишно движение сред звездите върху предварително разграфен лист паус-хартия -  2 т.
За правилен теоретичен подход при определяне на паралактичното движение на звездата в рамките на една година - 2 т.
За правилното разбиране на влиянието на собственото движение на звездата върху паралактичната елипса - 2 т.
За числовото определяне на стойностите на тези две движения на звездата - 2 т.
За определянето  на разстоянието до звездата - 2 т.
За изчисляване на тангенциалната скорост на звездата - 2 т.
За определянето на фотографската звездна величина на звездата - 1 т.
За определяне на абсолютната звездна величина на звездата - 1 т.
За дадени коментари на всички получени при решението на задачата данни, както и за вида на звездата - 2 т.