МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО
И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА
ПО АСТРОНОМИЯ
ІХ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
http://astro-olymp.org
ІV кръг - решения
Ученици старша възраст (до 17 г.)
1 задача. През лятото на 2026 г. астрономът Александър Куртенков извършва наблюдения от борда на геостационарна космическа станция. В свободното си време той дава консултации по GSM на участниците в астрономическия лагер “ The Dishes ” в източната част на Африка с координати φ = 0°, λ = 45°. В помощ на обучението, Александър решава да изпрати контейнер с научна информация и част от своите хранителни запаси до лагера.
С каква скорост и в каква посока трябва да се изхвърли контейнерът от станцията, така че да пада вертикално към Земята?
Какви са приблизително координатите на астрономическата обсерватория, над която се намира станцията? Приблизително в коя част на света е тя?
С каква минимална скорост на изхвърляне от станцията контейнерът може изобщо да достигне земната повърхност? Пресметнете големината на скоростта, с която контейнерът ще се удари в земната повърхност в този случай.
Влиянието на атмосферата да не се отчита.
Справочни данни:
Радиус на Земята – 6378 км
Маса на Земята – 6×1024 кг
Гравитационна константа – γ = 6.67×10–11 м3 /кг.с2
Решение:
Геостационарният спътник се движи в екваториалната равнина на Земята по посока на нейното околоосно въртене с период Т , равен на едно звездно денонощие, или 23 h 56 m . Радиуса на орбитата му r намираме от III закон на Кеплер:
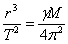
където М е масата на Земята, а γ е гравитационната константа.
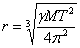 ≈ 43400 км ≈ 43400 км
За да пада контейнерът вертикално към Земята, той трябва да се изхвърли от спътника в посока, обратна на неговото движение, със скорост, равна по големина на скоростта на спътника. Тази скорост е:
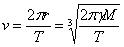 ≈ 3.08 км/с ≈ 3.08 км/с
За да оценим времето за падането на контейнера на Земята, предполагаме, че той се движи по много силно сплесната елиптична орбита около центъра на нашата планета с голяма полуос, равна на половината от радиуса на геостационарната орбита. Периодът на движение на контейнера по такава орбита Т1 можем да намерим отново с помощта на III закон на Кеплер:
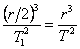
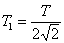
Времето за падането на контейнера ще бъде половината от този период, или:
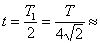 4 h 14 m 4 h 14 m
Но това е времето, за което контейнерът би паднал не до земната повърхност, а до центъра на Земята. Радиусът на Земята обаче, е само около 1/7 от радиуса на орбитата на спътника. Освен това за изминаването на тази последна 1/7 от пътя си до центъра на Земята, в случай, че цялата й маса беше съсредоточена в една точка там, контейнерът би изразходвал много малко време в сравнение с останалата част от пътуването си, защото би се движил с много голяма скорост. Ето защо можем да пренебрегнем това и да считаме, че времето за падане на контейнера на земната повърхност е приблизително 4 часа. За тези 4 часа Земята ще се завърти на около 4×15° = 60° на изток. Ето защо точката на падането на контейнера ще бъде на 60° западно от обсерваторията, над която „виси” геостационарният спътник. Географските координати на обсерваторията ще бъдат φ = 0°, λ = 105°. Това е някъде в Индонезия.
Минималната скорост на изхвърляне от контейнера v2 , при която той въобще ще достигне до земната повърхност, е скоростта, при която контейнерът би тръгнал да се движи по елипса с апогей върху геостационарната орбита и перигей върху земната повърхност. Голямата полуос на такава елипса би била:
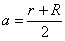
където R е радиусът на Земята. Скоростта на контейнера относно Земяата в апогей, т.е. в момента на изхвърлянето от спътника, ще бъде 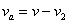 . Означаваме скоростта на контейнера в перигей с vp . Съгласно II закон на Кеплер: . Означаваме скоростта на контейнера в перигей с vp . Съгласно II закон на Кеплер:
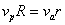
Приравняваме пълната механична енергия на контейнера в момента на хвърлянето му от спътника и в момента на достигането му до Земята:
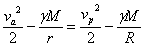
Масата на контейнера сме съкратили като множител във всеки от членовете на уравнението. От последните две уравнения получаваме:
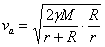
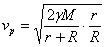
Скоростта, с която трябва да се изхвърли контейнерът от спътника, ще бъде:
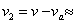 1.54 км/с 1.54 км/с
А скоростта, с която ще се удари в земната повърхност, ще бъде:
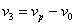
където  е линейната скорост на точка от екватора при околоосното въртене на Земята. е линейната скорост на точка от екватора при околоосното въртене на Земята.
v3 ≈ 10.0 км/с
2 задача. Вие сте светлозелени жители на Алфа, живеещи в съдружие с вашите виолетови съседи от Бета под лъчите на светилото Гама. Можете да виждате Бета само от едната страна на Алфа. Вашето алфа-денонощие съдържа 16 бета-цикъла. Всеки от тях е равен на времето между две преминавания на Блестящия бета-остров през централния меридиан на видимия диск на Бета. А времето между две обръщания на северната полярна бета-шапка към вас е равно на 15 бета-цикъла.
От гледна точка на жителите на Бета, колко бета-денонощия съдържа една година (една обиколка около Гама)?
Решение: От условието на задачата става ясно, че системата Алфа – Бета представлява двойна планета, или система от спътник и планета, обикалящи около звздата Гама. Бета се вижда само от едната страна на Алфа, което значи, че Алфа е винаги обърната с една и съща страна към Бета. Следователно периодът Ta* на околоосно въртене на Алфа е равен на периода, с който тя обикаля около Бета. Той се равнява на периода между две обръщания на северната полярна бета-шапка към Алфа, или на 15 бета-цикъла. Но това е сидеричният период на околоосно въртене на Алфа. А денонощието на Алфа, или нейният синодичен период Ta на околоосно въртене спрямо светилото Гама, е 16 бета-цикъла. Той е по-дълъг от Ta*, което означава, че околоосното въртене на Алфа става в същата посока, както обикалянето на системата Алфа-Бета около звездата Гама. Периода на орбитално движение на системата около Гама, или продължителността на годината Ta, можем да намерим от равенството:
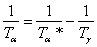
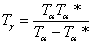
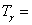 16 × 15 = 240 бета-цикъла 16 × 15 = 240 бета-цикъла
Годината, или времето за обиколка на системата Алфа-Бета около звездата Гама, съдържа 15 слънчеви алфа-денонощия по 16 бета-цикъла, или 16 звездни алфа-денонощия по 15 бета-цикъла.
В един сидеричен период Ta* на обикаляне на Алфа около Бета (времето между две обръщания на северната полярна бета-шапка към Алфа) има 15 бета-периода. Това е броят на завъртанията на Бета около нейната ос за един сидеричен период на обикаляне на Алфа около Бета. Но това са околоосните завъртания на Бета за наблюдател от Алфа. Относно неподвижните звезди броят на околоосните завъртания на Бета ше бъде с 1 по-голям, т.е. 16. Годината Тγ съдържа 16 сидерични или звездни алфа-периода. Следователно общият брой на звездните бета-денонощия в годината е 16 алфа-периода в една година ×16 завъртания на Бета в един алфа-период = 256. Това са звездните бета-денонощия в една година. Слънчевите бета-денонощия в годината ще бъдат с 1 по-малко от звездните. Ето защо, за жителите на Бета в годината има 255 денонощия.
3 задача. С методите на звездната интерферометрия е измерен ъгловият диаметър на звезда с блясък 4m.7. Големината на диаметъра е 0.004″ (дъгови секунди). Спектроскопичните наблюдения на звездата показват, че жълтата линия на натрия (5890 ангстрьома) има две компоненти – ярка и слаба. Дължината на вълната на слабата компонента се променя синусоидално с амплитуда ± 0.6 ангстрьома и период 30 години, а веднъж в рамките на този период слабата линия изчезва за интервал от 230 дни. Оценете разстоянието до звездата, нейната маса и температура на повърхността. Какъв тип звезда е това?
Решение: Слабата компонента на натриевата линия в спектъра на звездата се създава от звезда-спътник, която е значително по-малка от главната звезда. Орбиталният период на спътника около главната звезда е T = 30 години. От амплитудата Δλ = ± 0.6 Å на изменение на дължината на вълната на натриевата линия с λ = 5890 Å можем да намерим линейната скорост на движение на спътника:
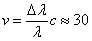 км/с км/с
където с е скоростта на светлината. Изчезването на слабата компонента на натриевата линия се дължи на затъмнение на спътника от главната звезда. Ако приемем, че затъмнението е централно, то от продължителността му t = 230 дни можем да пресметнем диаметъра на главната звезда:
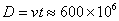 км км
Като имаме предвид ъгловия размер на звездата 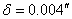 , изчисляваме разстоянието до нея: , изчисляваме разстоянието до нея:
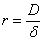
За да го получим направо в парсеци, превръщаме D в астрономически единици:
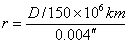 =1000 pc =1000 pc
Като знаем орбиталния период на спътника и неговата скорост, можем да намерим радиуса на неговата орбита около главната звезда:
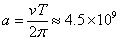 км = 30 AU км = 30 AU
Предполагаме, че масата на спътника е много по-малка от масата на главната звезда. От III закон на Кеплер за масата на главната звезда М в слънчеви маси намираме:
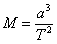
Тук а е в астрономически единици, а Т в години.
М = 30 слънчеви маси
Забелязваме, че видимата звездна величина на звездата е приблизително равна на абсолютната звесдна величина на Слънцето. Разстоянието до звездата обаче е 1000 парсека, или 100 пъти по-голямо от стандартното разстояние от 10 pc , спрямо което се дефинира абсолютната звездна величина. Следователно светимостта L на звездата е
1002 = 10000 пъти по-висока от светимостта на Слънцето LS . Ако означим с 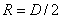 и RS= 700 000 км радиусите на звездата и на Слънцето, а с T и TS – техните температури, то можем да напишем: и RS= 700 000 км радиусите на звездата и на Слънцето, а с T и TS – техните температури, то можем да напишем:
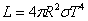
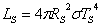
Където s е константата на Стефан-Болцман. Разделяме почленно двете равенства:
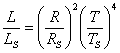
Като знаем, че температурата на Слънцето е 6000 К, за температурата на звездата получаваме:
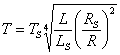
Т ≈ 2900 К
Звездата е много по-масивна от Слънцето и е в края на своята еволюция – превърнала се е в червен свръхгигант.
Практическа задача. Двойнствеността на спектрално двойните звезди се установява чрез спектрални наблюдения. В таблицата са дадени данни за лъчевите скорости на компонентите на спектрално двойната звездна система p от Корабни платна .
Изследвайки кривата на лъчевите скорости, покажете приблизително как са ориентирани орбитите на компонентите й спрямо наблюдател на Земята, като приемете, че зрителният лъч лежи в орбиталната равнина. Изчислете масите на двете компоненти в единици слънчеви маси.
No |
T |
V1
km/s |
V2
km/s |
1 |
0 d 00.0 h |
23.1 |
13.2 |
2 |
0 d 14.4 h |
6.6 |
39.6 |
3 |
0 d 20.5 h |
1.2 |
52.8 |
4 |
1 d 06.8 h |
-19.8 |
85.8 |
5 |
1 d 11.9 h |
-39.6 |
98.7 |
6 |
1 d 19.5 h |
-46.2 |
92.4 |
7 |
1 d 23.2 h |
-36.3 |
72.6 |
8 |
2 d 07.4 h |
-4.9 |
42.9 |
9 |
2 d 15.6 h |
9.9 |
33.1 |
10 |
3 d 01.8 h |
16.5 |
23.2 |
11 |
3 d 18.6 h |
26.4 |
8.2 |
12 |
4 d 18.8 h |
36.3 |
-3.3 |
13 |
5 d 21.5 h |
39.6 |
-6.6 |
14 |
6 d 20.1 h |
37.9 |
-9.9 |
15 |
8 d 04.8 h |
36.3 |
-3.3 |
16 |
9 d 09.5 h |
26.4 |
8.2 |
17 |
9 d 19.8 h |
23.1 |
13.2 |
18 |
10 d 06.1 h |
14.9 |
23.1 |
19 |
10 d 15.2 h |
3.3 |
36.3 |
20 |
11 d 02.5 h |
-19.8 |
62.7 |
Решение: Построяваме кривите на изменеие на лъчевите скорости на двете компоненти на системата. Виждаме, че на високия остър пик на лъчевата скорост на компонентата 1 съответства дълбок стръмен спад на лъчевата скорост на компонентата 2. На полегатия плавен спад на лъчевата скорост на звездата 1 съответства полегато плавно увеличение при звездата 2. Това се дължи на факта, че около моментите на минимумите и максимумите на лъчевите скорости направлението на действителните скорости на звездите е близко до направлението на зрителния лъч от земния наблюдател. Освен това, острите пикове и спадове отразяват бързото и силно нарастване на радиалната компонента на скоростта на всяка от звездите около перицентъра на нейната орбита относно центъра на масите на системата. Полегатите пикове и спадове отразяват движението на компонентите около апоцентровете на техните орбити. Симетричността на пиковете и спадовете говори за това, че всъщност скоростите на звездите в самите перицентрове и в апоцентровете на техните орбити практически съвпадат по направление със зрителния лъч. Следователно големите оси на елиптичните орбити на звездите са разположени перпендикулярно на зрителния лъч от земния наблюдател. Зрителният лъч лежи в равнината на орбитите. Следователно лъчевите скорости в перицентровете и апоцентровете на елиптичнита орбити на звездите, измерени по върховите стойности на графиката, са равни на действителните скорости на звездите в тези точки.
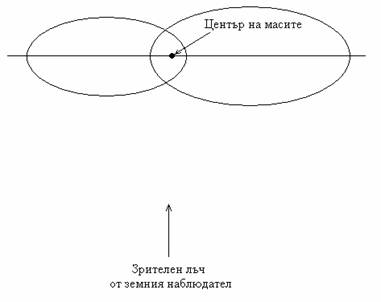
Прекарваме хоризонтална линия през точките, където двете графики на лъчевите скорости се пресичат. Нивото на тази линия определя лъчевата скорост, с която се движи центърът на масите на двойната звездна система относно нас. Тя е vС = 20 км/с. Когато определяме лъчевата скорост на коя да е от звездите в даден момент чрез измерване и отчитане по графиката, от тази измерена стойност винаги вадим vС , за да получим лъчевата скорост на звездата относно центъра на масите.
Означаваме с vp1 , va1 , vp2 , va2 скоростите в перицентъра и в апоцентъра съответно на зведата 1 и на звездата 2. От измерванията, като приведем стойностите към движение относно центъра на масите на системата, получаваме:
vp1 = 80 км/с
va1 = 30 км/с
vp2 = 65 км/с
va2 = 20 км/с
Отношението на масите на двете звезди М1 и М2 е:
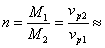 0.8 (1) 0.8 (1)
Разглеждаме движението примерно на звездата 2 относно звездата 1. В координатна система, в която звездата 1 е неподвижна, звездата 2 описва около нея относителна елипса със следните параметри:
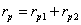
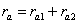
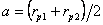
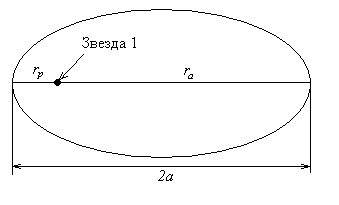
Скоростите на движение на звездата 2 относно звездата 1 в перицентъра и апоцентъра на относителната елипса са съответно:
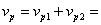 145 км/с (2) 145 км/с (2)
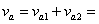 50 км/с (3) 50 км/с (3)
Съгласно ІІІ закон на Кеплер:
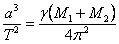
Орбиталния период определяме също по графиката:
Т = 9.8 денонощия. Въвеждаме следното означение:
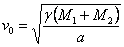 (4) (4)
Това е скоростта, с която звездата 2 би се движила по кръгова орбита с радиус а около звездата 1. Тогава:
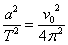 (5) (5)
От ІІ закон на Кеплер: 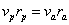 , и от формулата: , и от формулата:
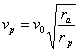
като използваме (2) и (3), определяме:
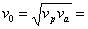 85.15 км/с 85.15 км/с
Оттук и от равенствата (5), (4) и (1) намираме последователно:
 11.48×106 км 11.48×106 км
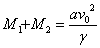
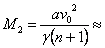 0.70×1030 кг ≈ 0.35 сл. маси 0.70×1030 кг ≈ 0.35 сл. маси
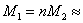 0.55×1030 кг ≈ 0.28 сл. маси 0.55×1030 кг ≈ 0.28 сл. маси
|