МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО
И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА
ПО АСТРОНОМИЯ
ХI НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
http://astro-olymp.org
ІV кръг, теоретичен тур - решения
Ученици младша възраст (до 16 г.)
Задача 1. Кралска яхта
Велик и важен крал пътува с кралската си яхта по екватора. Един придворен, по заповед на краля, се грижи часовникът в каютата му винаги да е настроен по поясното време на пояса, в който се намират в момента. Кралят иска всеки ден да получава закуската си в 8 часа сутринта. Но всяка сутрин, точно преди да стане 8 часа, влиза придворният и връща часовника на 7 часа. Така кралят винаги трябва да чака още един час, докато му донесат закуската. В каква посока и с каква скорост се движи яхтата? Радиусът на Земята е 6378 км.
В изблик на силно раздразнение кралят заповядва на капитана да подкара яхтата с двойно по-голяма скорост. Какво ще се случи с режима му на ставане и закусване тогава?
Решение:
Земята се върти около своята ос от запад на изток. Когато се движим в същата посока, т.е. на изток, ние се “надбягваме” с точките от земната повърхност и срещаме изгревите на Слънцето все по-рано и по-рано. Обратно, когато се движим на запад, ние “бягаме” от изгряващото Слънце и изгревите настъпват все по-късно и по-късно. Всяка сутрин придворният връща часовника на краля с 1 час назад, за да показва поясно време. Следователно яхтата се движи на запад. Това означава също, че за едно денонощие яхтата изминава разстояние колкото е ширината на един часови пояс. Часовите пояси по земното кълбо са 24, като всеки от тях обхваща 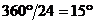 . По екватора това отговаря на разстояние . По екватора това отговаря на разстояние 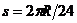 , където R е радиусът на Земята. Така полученото разстояние се изминава от яхтата за едно денонощие от 24 часа плюс още един час, или за t = 25 часа. Скоростта на яхтата е: , където R е радиусът на Земята. Така полученото разстояние се изминава от яхтата за едно денонощие от 24 часа плюс още един час, или за t = 25 часа. Скоростта на яхтата е:
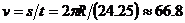 км/час. км/час.
Движейки се с двойно по-голяма скорост, яхтата ще изминава два часови пояса за 25 часа. Да предположим, че в 8 часа сутринта някой ден яхтата се намира в началото на един часови пояс. В 20:30 ч. вечерта яхтата ще е на границата със следващия часови пояс. Тогава слугата ще премести часовника с 1 час назад и той ще показва 19:30 ч. В 8 ч. сутринта на следващия ден яхтата ще премине границата със следващия часови пояс и часът ще стане 7. Следователно кралят ще чака 1 час закуската си. По-късно в 19:30 ч. яхтата ще пресече следващата граница и часът ще стане 18:30. В 7 ч. на следващата сутрин тя ще е на следващата граница и поясното време ще е 6 часа, но кралят няма да си чака закуската, защото още ще спи. В 18:30 яхтата ще навлезе в следващия часови пояс и часът ще стане 17:30. След това в 6 ч. сутринта ще е на границата на следващия. Това означава, че кралят няма да чака закуската си, отново защото още ще спи. Вижда се, че при два пъти по-голяма скорост режимът на закусване на краля ще бъде различно засегнат в различните дни.
Интерес представляват дните, в които яхтата ще е на границата между два часови пояса в 9 часа. Час преди това кралят вече ще е закусил. Но в 9 ч. часовникът ще бъде върнат на 8 часа и кралят ще трябва закуси още веднъж. Друг възможен такъв случай е когато границата между поясите се пресича в 8:30. Тогава, тъкмо след закуската на краля часовникът ще бъде върнат на 7:30 и половин час по-късно кралят пак ще трябва да получи втора закуска.
Задача 2. Възможна комета
Известният наблюдател на комети от Русе Момчил Молнар изпратил спешна телеграма в Международния астрономически съюз, че е открил нова комета. Неговите пресмятания, извършени с логаритмична линийка, показали, че кометата има афелийно разстояние 820 млн. км и период на обиколка около Слънцето – 2 години.
Оценете верността на резулатите на младия астроном и възможостта да се увенчае със световна слава за своето откритие. (1 AU = 150 x 106 km).
Решение:
Тъй като кометите имат силно елиптични орбити, то тяхното афелийно разстояние е много по-голямо от перихелийното. Но колкото и малко да е перихелийното разстояние на кометата, за голямата полуос на орбитата й а можем да напишем следния израз:
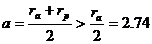 AU AU
където ra и rp са афелийното и перихелийното разстояние на кометата. От третия закон на Кеплер, записан за две тела в Слънчевата система, едно от които е Земята, можем да дадем оценка за орбиталния период на една комета:
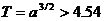 години години
Следователно описаната в задачата комета не би могла да съществува.
Задача 3. Определяне на географската ширина.
Теди и Миро потеглят на морско пътешествие. За нещастие те забравят ъгломерните си инструменти и всякакви справочни материали на брега, рискувайки да се загубят в безкрайната шир. Теди открива в трюма на кораба стар алтазимутален телескоп. Миро си спомня, че деклинацията на любимата му звезда Алрай е 78° и измерва разликите във височините на тази звезда в горна и долна кулминация. Разликата се оказва 40°.
Помогнете на пътешествениците и определете каква е тяхната географска ширина.
Решение:
Ще разгледаме две възможности. Първата е както горната, така и долната кулминация да се случи на север от зенита.
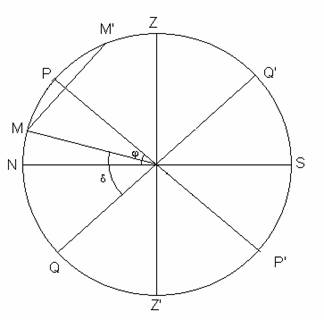
На чертежа са означени хоризонтът на наблюдателя NS, небесният екватор QQ’ и паралелът MM’, по който се движи звездата. Нейната деклинация е d, а j е географската ширина на мястото. Дъгата NM представлява височината на звездата в долна кулминация, а дъгата NM’ височината на звездата н горна кулминация. В сила са следните съотношения:
МР = М’Р = 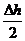 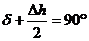
където 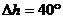 трябва да е разликата във височините. Но това условие е неизпълнимо и следователно тази конфигурация не е възможна. трябва да е разликата във височините. Но това условие е неизпълнимо и следователно тази конфигурация не е възможна.
Втората възможност е горната кулминация да е на юг (M’), а долната на север от зенита (M).

Височините на звездата над хоризонта при двете кулминации са съответно h1 и h2 . От чертежа се вижда, че трябва да е изпълнено:
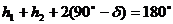
Оттук следва:
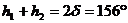
Същевременно трябва да е в сила:
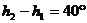
Решението на системата от последните две уравнения дава:
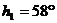 ; ; 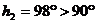 , ,
което очевидно е лишено от смисъл. Изводът е, че разликата във височините не е измерена правилно.
Задача 4. Пасаж на Луната
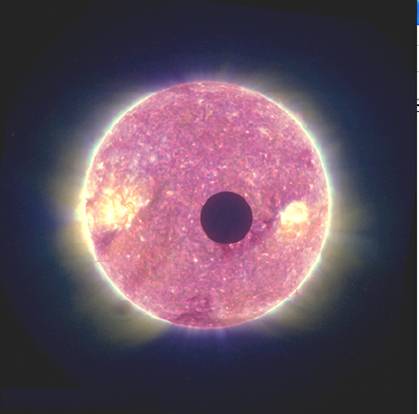
Снимката е направена на 10 юни 2008 г. На нея се вижда Луната на фона на Слънцето. На какво разстояние се намира космическият апарат от Луната? А от Слънцето?
Решение:
На схемата с T е означено положението на Земята, а с L – на Луната.
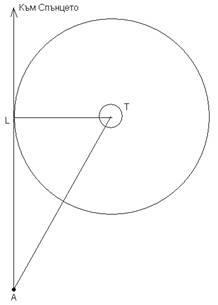
От дадената ни страница за месец юни 2008 г. от Астрономияеския алманах виждаме, че на 10 юни Луната е била в първа четвърт. Ето защо положението на апарата е в т. А на схемата. Очевидно той не е много далеч от Земята. Това означава, че видимият от него ъглов диаметър на Слънцето е приблизително същият, какъвто е и за земния наблюдател. Измерваме в милиметри диаметрите на Слънцето и Луната върху снимката:
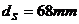 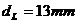
Знаем, че при наблюдение от Земята видимите ъглови диаметри на Слънцето и Луната са приблизително еднакви. Следователно колкото пъти видимият от космическия апарат ъглов диаметър на Луната е по-малък от този на Слънцето, толкова пъти космическият апарат е по-отдалечен от Луната, отколкото е отдалечена Земята:
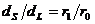
където r1 е разстоянието от спътника до Луната, а r0 от Земята до Луната. Оттук получаваме:
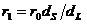
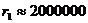 км км
От триъгълника ATL и Питагоровата теорема за разстоянието от космическия апарат до Земята пресмятаме:
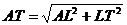
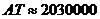 км км
Задача 5. Планета около далечна звезда
Наблюдаван е пасаж на екзопланета пред диска на звездата, около която тя обикаля. Блясъкът на звездата се променя с 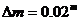 . Намерете колко пъти радиусът на звездата е по-голям от радиуса на планетата. Звездата е от Главната последователност, има температура 8200 К и светимост 14 пъти по-голяма от светимостта на Слънцето. Намерете радиуса на планетата в километри. Радиусът на Слънцето е 700 000 км, а температурата му е 5800 К. . Намерете колко пъти радиусът на звездата е по-голям от радиуса на планетата. Звездата е от Главната последователност, има температура 8200 К и светимост 14 пъти по-голяма от светимостта на Слънцето. Намерете радиуса на планетата в километри. Радиусът на Слънцето е 700 000 км, а температурата му е 5800 К.
Решение:
По време на пасажа блясъкът на звездата намалява
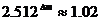 пъти. пъти.
Нека с R да означим радиуса на звездата, a c r радиуса на планетата. Когато планетата не е пред звездата, излъчващата площ на диска на звездата е 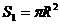 . По време на пасажа тази площ е . По време на пасажа тази площ е 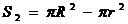 . Блясъкът на звездата нямалява именно пради това, че планетата е тъмна и закрива част от излъчващия диск на звездата. Следователно можем да запишем, че отношението на осветеностите Е1 и Е2 , които създава звездата в двата случая е равно на отношението на двете излъчващи площи: . Блясъкът на звездата нямалява именно пради това, че планетата е тъмна и закрива част от излъчващия диск на звездата. Следователно можем да запишем, че отношението на осветеностите Е1 и Е2 , които създава звездата в двата случая е равно на отношението на двете излъчващи площи:
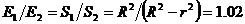
Оттук получаваме 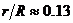 . Следователно планетата е с около 7.7 пъти по-малък радиус отколкото звездата. Oзначаваме с T – температурата на звездата, а с R0 и T0 радиуса и температурата на Слънцето. За светимостите на звездата и Слънцето L и L0 е в сила: . Следователно планетата е с около 7.7 пъти по-малък радиус отколкото звездата. Oзначаваме с T – температурата на звездата, а с R0 и T0 радиуса и температурата на Слънцето. За светимостите на звездата и Слънцето L и L0 е в сила:
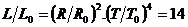
Оттук намираме 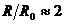 . По-нататък изчисляваме: . По-нататък изчисляваме: 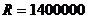 km. и km. и 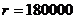 km. km.
Ученици старша възраст (до 18 г.)
Задача 1. Изгрев на Слънцето
В един мартенски ден младият астрономЧавдар Дуцов от София (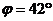 ) наблюдава изгрев на Слънцето точно на изток. Той се опитва да предскаже какъв ще е азимутът на Слънцето в момента на залеза му същия ден. Пресметнете това и вие за два случая – без отчитане и с отчитане на рефракцията. ) наблюдава изгрев на Слънцето точно на изток. Той се опитва да предскаже какъв ще е азимутът на Слънцето в момента на залеза му същия ден. Пресметнете това и вие за два случая – без отчитане и с отчитане на рефракцията.
Решение:
Ако не отчитаме рефракцията, можем да приемем, че по време на изгрева Слънцето е било точно на небесния екватор. Тогава то е имало деклинация 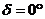 . С течение на деня неговата деклинация е нараствала, защото е казано, че денят е от месец март, т.е. това е денят на пролетното равноденствие и Слънцето навлиза в северната небесна полусфера. Средната ъглова скорост на Слънцето по еклиптиката е . С течение на деня неговата деклинация е нараствала, защото е казано, че денят е от месец март, т.е. това е денят на пролетното равноденствие и Слънцето навлиза в северната небесна полусфера. Средната ъглова скорост на Слънцето по еклиптиката е 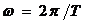 , където Т = 1 година е орбиталният период на Земята. По време на равноденствие Слънцето се движи под ъгъл , където Т = 1 година е орбиталният период на Земята. По време на равноденствие Слънцето се движи под ъгъл 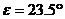 спрямо небесния екватор (наклонът на еклиптиката към екватора). Тогава скоростта, с която то си изменя деклинацията, е спрямо небесния екватор (наклонът на еклиптиката към екватора). Тогава скоростта, с която то си изменя деклинацията, е 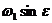 . .
Можем да считаме, че продължителността на деня е била 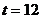 h., тъй като деклинацията на Слънцето се е изменила незначително в рамките на този интервал. Оттук следва, че деклинацията му при залеза е h., тъй като деклинацията на Слънцето се е изменила незначително в рамките на този интервал. Оттук следва, че деклинацията му при залеза е 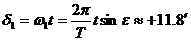

Ъгълът, под който екваторът пресича хоризонта в точката запад (W), е  . Под този ъгъл изгряват и залязват всички светила за София. Следователно, можем да запишем връзката: . Под този ъгъл изгряват и залязват всички светила за София. Следователно, можем да запишем връзката: 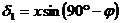 , където х е отстоянието на точката на залеза от точката запад по хоризонта. Оттук намираме: , където х е отстоянието на точката на залеза от точката запад по хоризонта. Оттук намираме:
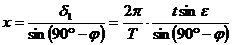
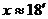
Ако се отчита рефракцията, трябва да се има предвид, че при изгрева деклинацията на Слънцето не е 0°. На фигурата е показана схема на изгрева на Слънцето. В момента на изгрева то в действителност се намира на определена дълбочина под хоризонта, която е равна на ъгъла на рефракция 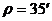 . .

От чертежа се вижда, че деклинацията на Слънцето тогава е била
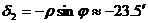 . .
Тук отново ще считаме, че денят продължава 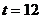 h време. Следователно, деклинацията на Слънцето при залеза ще е: h време. Следователно, деклинацията на Слънцето при залеза ще е:
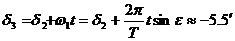
На следващия чертеж е показана схемата на залеза:

Слънцето залязва когато височината му под хоризонта е равна на r. Деклинацията на Слънцето ще се е повишила с 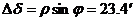 . Аналогично на първия случай намираме отстоянието на точката на залеза от точката запад: . Аналогично на първия случай намираме отстоянието на точката на залеза от точката запад:
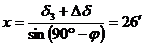
Тук също точката на залез ще е южно от точката запад.
Задача 2. Пепелна светлина
Сравнете звездните величини, които се създават от пепелната светлина на Луната в новолуние за земния наблюдател и на Земята в «новоземие» за лунния наблюдател. Не отчитайте светенето на земната атмосфера и светенето на тънките сърпове на двете тела при тези фази.
Решение:
Нека с E0 означим осветеността, която Слънцето създава върху Земята (тя е практически същата като осветеността върху Луната). Потокът слънчева светлина, попадащ върху Земята, ще бъде:
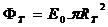
където RT е радиусът на Земята. Ако AT е отражателната способност на Земята, то количеството отразена от нея слънчева светлина ще бъде:
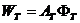
Отразената от Земята слънчева светлина ще създава върху Луната осветеност:
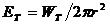
където r е разстоянието от Земята до Луната. Потокът земна светлина, попадащ върху Луната, ще бъде:
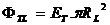
където RL е радиусът на Луната. Количеството земна светлина, което Луната ще отразява, е:
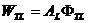
Така Луната ще създава осветеност на Земята, която ше бъде:
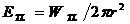
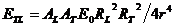
Това е блясъкът на пепелната светлина на Луната.
По аналогичен начин можем да получим осветеността ELT , която Земята създава върху Луната, преотразявайки отразената от Луната слънчева светлина. При това се убеждаваме, че 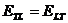 . Пепелната светлина от Земята, получена върху Луната е еднаква по блясък с пепелната светлина на Луната за земния наблюдател. . Пепелната светлина от Земята, получена върху Луната е еднаква по блясък с пепелната светлина на Луната за земния наблюдател.
Задача 3. Интерферометрия на звезда.
С методите на интерферометрията е измерен ъгловият диаметър на звезда, който се оказва 0’’,004. Блясъкът на звездата е 4.7m. Спектроскопичните наблюдения на тази звезда показват, че жълтата линия на натрия (5890 Å) има две компоненти – ярка и слаба, при което дължината на вълната на слабата компонента се променя синусоидално с амплитуда 0,6 Å и период 30 години. Един път за целия период слабата линия на натрия престава да се вижда в продължение на 230 дни.
Определете разстоянието до звездата, нейната маса и температурата на повърхноста й. Към кой тип звезди можем да я причислим?
Решение:
Нека с L да означим светимостта на звездата, а с r разстоянието до нея. Осветеността, която звездата създава за нас е:
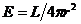
Светимостта на звездата е:
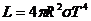
където R и T са нейният радиус и температурата й. Оттук получаваме:
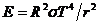
Понеже видимият ъглов диметър на звездата е 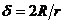 , то: , то:
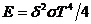
Знаем слънчевата константа 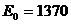 W/m2 и видимата звездна величина на Слънцето W/m2 и видимата звездна величина на Слънцето 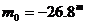 . Ако . Ако 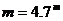 е дадената ни звездна величина на звездата, то: е дадената ни звездна величина на звездата, то:
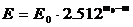
Така за температурата получаваме:
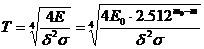
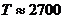 K K
Ярката компонента на спектралната линия принадлежи на самата звезда, а слабата на неин спътник, имащ много по-малка светимост от нея. Изменението на слабата линия се дължи на орбителното движение на спътника около звездата. Амплитудата на промяната на дължината на вълната съответства на максималната стойност v на лъчевата скорост на спътника. Означаваме тази амплитуда с 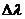 , с , с 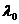 – лаборатнорната дължина на вълната, а с с – скоростта на светлината. Съгласно формулата за изменението на дължината на вълната поради ефекта на Доплер при движение на източника със скорост v : – лаборатнорната дължина на вълната, а с с – скоростта на светлината. Съгласно формулата за изменението на дължината на вълната поради ефекта на Доплер при движение на източника със скорост v :
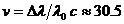 km/s km/s
Тъй като дължината на вълната на слабата спектрална линия се изменя синусоидално, можем да предположим, че спътникът има кръгова орбита около звездата и да приемем, че зрителният лъч от нас към нея лежи приблизително в орбиталната равнина на спътника. Така че можем да считаме v за равна на орбиталната скорост на спътника около звездата. Слабата линия периодично изчезва за време 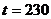 d. Това става, когато спътникът преминава зад звездата и всъщност изминава нейния диметър D. Oттук намираме: d. Това става, когато спътникът преминава зад звездата и всъщност изминава нейния диметър D. Oттук намираме:
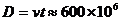 km km
Като знаем видимия ъглов диаметър на звездата, намираме разстоянието до нея:
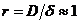 kpc kpc
От разстоянието и видимата звездна величина на звездата намираме абсолютната й звездна величина:
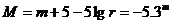
Звездата има неимоверно висока светимост и много ниска температура. Следователно, тя е огромен и хладен червен гигант.
За да намерим масата M* на звездата, използваме ІІІ закон на Кеплер. Заяписваме закона за случая, когато радиусът а на орбитата на спътника се измерва в астрономически единици, неговият орбитален период Р в години (по условие  години), а масата на звездата – в слънчеви маси: години), а масата на звездата – в слънчеви маси:
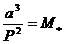
Радиуса на орбитата намираме от съотношението:
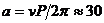 АU АU
Накрая за масата получаваме:
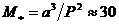 слънчеви маси слънчеви маси
Задача 4. Точка на стоене
Участникът в Международната олимпиада по астрономия и бъдещ астроном Александър Куртенков ви кани да споделите с него удоволствието от едно теоретично изследване. Той е забелязал, че моментът, в който една външна планета е в квадратура, не съвпада точно с момента, в който става преходът на планетата между право и обратно видимо движение. Намерете разликата между тези два близки момента от време като функция на радиуса на планетната орбита около Слънцето. Изведете приблизителна формула само за случая, когато планетата е много отдалечена от Слънцето.
Решение:
На фигурата с S е означено положението на Слънцето, с T1 – положението на Земята и с P – положението на външна планета в квадратура.
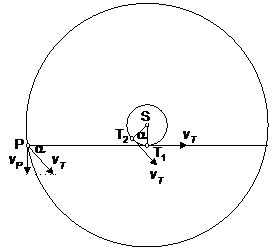
Когато далечна планета се намира в квадратура, нейната скорост vP е приблизително перпендикулярна на земната орбитална скорост vT (Земята в положение T1). Но тогава планетата няма да е в точката на стоене. Ъгловата скорост на видимото й движение по небесната сфера няма да е нула. Тя ще стане нула, когато Земята е в малко по-друго положение (T2) – такова, че компонентата на земната линейна скорост по направление на движението на планетата да стане равна на орбиталната скорост на планетата. Тогава “напречната” скорост на относително движение на планетата спрямо Земята (по направление перпендикулярно на зрителния лъч за земен наблюдател) ще стане нула.
Използваме приближението, че поради голямата отдалеченост на планетата ъгълът Земя – планета – Слънце е много малък. По същото съображение пренебрегваме движението на планетата по нейната орбита между моментите, когато Земята е в положение Т2 и Т1. Моментът на стоене на планетата може да се случи малко преди или малко след момента, когато тя е в квадратура. За определеност разглеждаме случая, в който моментът на стоене настъпва малко преди квадратурата. Нека Земята, намираща се в точка Т2, е отклонена на ъгъл a по своята орбита спрямо положението си Т1, когато външната планета е в квадратура. Нейната скорост vTтогава сключва същия ъгъл с линията T1P. Смятаме, че скоростта на планетата vP в този момент e приблизително перпендикулярна на линията T1P. Така можем да напишем:
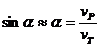
Търсеният от нас интервал от време между моментите, когато Земята е в T1 и Т21 , ще бъде:
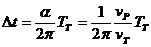
където ТT е орбиталният период на Земята около Слънцето, равен на 1 година. Ако rT и rP са радиусите на орбитите на Земята и на планетата, а TP е орбиталният период на планетата:
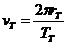
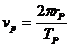
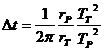
Съгласно третия закон на Кеплер:
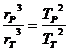
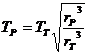
Следователно:
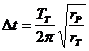 
Ако rP е в астрономически единици, а t е в години:
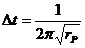 години години
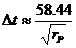 дни дни
Задача 5. Лъчеви скорости.
През първата половина на май 2003 г., в малка област на небето, са проведени спектрални наблюдения и са получени следните максимални стойности на лъчевите скорости: 44,8 км/с, 41,2 км/с, 38,4 км/с, 35,7 км/с, 40.1 км/с и 14.9 км/с. След три години в първата половина на юни са проведени отново набдения на същия обект, но резултатите се оказват различни: 17,3км/с, 13,7 км/с, 10,9 км/с, 8,2 км/с, 12.6 км/с и –12.6 км/с . Какво са наблюдавали астрономите? Обосновете своя отговор с пресмятания.
Решение:
Забелязваме, че разликата между лъчевите скорости, измерени в двата момента, е една и съща за всяка от точките (обектите). Не е възможно това да са лъчевите скорости, измерени в различни точки от някаква галактика. Типичните скорости на звездите от галактиката са значително по-големи. Дори и да става въпрос за малка галактика, в която звездите не се движат с големи скорости относно нейния център, то лъчевите скороти на отделните обекти в нея щяха да съдържат като компонента лъчевата скорост на галактиката като цяло относно нас, която със сигурност би била много по-голяма.
Не е възможно това да са лъчевите скорости на някакви звезди в малка област от нашата галактика, защото тогава не би могла да се обясни еднаквата разлика от 27,5 км/сек, която се получава за двата момента от време.
Можем да предположим, че първите четири числа от поредицата са лъчевите скорости на планети около друга звезда, а последните две стойности са лъчевите скорости на две диаметрално противоположни точки от диска на звездата. Системната разлика от 27,5 км/сек можем да обясним с хипотезата, че звездата влиза в състава на двойна звездна система и се движи около центъра на масите на системата. Но все още не е възможно да се получат поотделно спектри на две диаметрално противоположни области от видимия диск на звезда. Остава предположението, че това е система от много по-близки обекти в рамките на Слънчевата система. Последните две стойности най-вероятно се отнасят до противоположни точки от видимия диск на въртяща се планета, а първите четири – до орбиталните скорости на нейните спътници. Поради наличието на поне четири спътници, безспорно това е някоя от големите планети – гиганти. Очевидно при второто наблюдение, планетатта е имала нулева лъчева скорост. Следователно, тогава тя е била в опозиция. Три години и един месец по-рано лъчевата скорост на планетата е била +27,5 км/сек. Тази стойност е близка до орбиталната скорост на Земята, което означава, че планетата тогава е била близо до западна квадратура. Да проверим това за Юпитер.
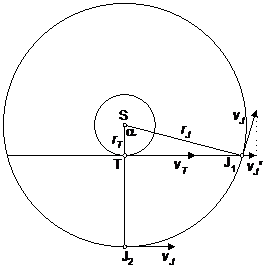
На чертежа с S сме означили Слънцето, с Т – Земята, а с J1 и J2 – положенията на Юпитер в западна квадратура и в опозиция. Като знаем орбиталните периоди на Земята и Юпитер TT и TJ , можем да намерим синодичния период на Юпитер:
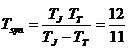 години години
 години години
Известни са ни също и радиусите на орбитите на Земята и Юпитер rT и rJ , от които можем да пресметнем ъгъла a:
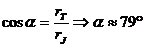
Периодът от време от западна квадратура до опозиция е:
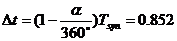 години години
От май 2003 година до юни 2006 година са изминали 3 години и 1 месец или приблизително 3.083 години. Това е два пъти синодичния период на Юпоитер плюс още 0.9 години, което е приблизително равно на 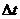 . Следователно планетата е Юпитер. Разликата от 2.5 км/с в орбиталната скорост на Земята идва идва оттам, че в квадратура Юпитер има такава компонента на скоростта, насочена към нас. . Следователно планетата е Юпитер. Разликата от 2.5 км/с в орбиталната скорост на Земята идва идва оттам, че в квадратура Юпитер има такава компонента на скоростта, насочена към нас.
В правилността на предположението за Юпитер се убеждаваме отново, като пресметнем линейната скорост на точки от екватора на планетата, която се оказва близка до 12 км/сек. В същото време от астрономическия алманах пресмятанията показват, че четирите спътници са Йо, Европа, Ганимед и Калисто. |