МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО
И НАУКАТА
ЦЕНТРАЛНА КОМИСИЯ ЗА ОРГАНИЗИРАНЕ НА ОЛИМПИАДАТА
ПО АСТРОНОМИЯ
ХIІ НАЦИОНАЛНА ОЛИМПИАДА ПО АСТРОНОМИЯ
http://astro-olymp.org
ІV кръг, теоретичен тур - решения
Ученици младша възраст (до 16 г.)
Задача 1. Котешко око (Адаптирана от ESO Exercieses). Красивата планетарна мъглявина Котешко око (Фиг. 1) се намира в съзвездието Дракон. Изображенията на мъглявината, получени в различни години от телескопа “Хъбъл”, дават възможност да се проследи разширяването на мъглявината в космическото пространство. Ние ще разгледаме увеличаването на малката полуос на елипсоидалното образувание Е 25, означено на Фиг. 2. На Фиг. 3 са дадени две изображения на мъглявината в еднакъв мащаб, получени на 18.Х.1994 г. и на 17.VІІІ.1997 г. При сравняването им разширението на мъглявината не може да се забележи и да се измери пряко. Но разделителната способност на телескопа “Хъбъл” позволява да се получи резултат по друг начин. При обработка с компютър размерите на първото изображение се увеличават с коефициент F, малко по-голям от единица. После се прилага математическа процедура на “изваждане” на първото изображение от второто. Резултатите за различни пробни стойности на F са дадени на Фиг. 4. По спектрални изследвания и теоретично моделиране на мъглявината е определено, че малката полуос на образуванието Е 25 се увеличава със скорост 16.4 км/сек.
• Като използвате предоставената ви информация, определете разстоянието до мъглявината Котешко око.
• Оценете приблизително възрастта на мъглявината.
Решение:
Ако след умножението на размерите по фактор F, снимката от 1994 г се окаже еднаква с тази от 1997 г, то при изваждането на двете изображения би трябвало да се получи остатъчен кадър, на който да няма почти нищо. Следователно факторът, с който ъгловият размер на мъглявината се е увеличил за дадения период от време, е този, при който остатъчният кадър е най-празен. Виждаме, че това се реализира при кадъра, получен чрез умножение с фактор 1,0025. Все пак и на този кадър има някакво остатъчно избражение. Можем да предположим, че точната стойност на фактора е между 1,0025 и 1,0030, примерно 1,00275. За интервала от време между 18.Х.1994 г. и 17.VIII.1997 г. (t = 1064 дни) ъгловият, а и линейният размер на малката полуос на Е 25 се е увеличил с 0,275%. От Фигура 1 измерваме малката полуос на елиптичното образувание Е 25 в милиметри и като използваме дадения ни мащаб в дъгови секунди, получаваме нейния видим ъглов размер 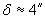 . Това означава, че промяната на малката полуос за дадения интервал от време ще бъде . Това означава, че промяната на малката полуос за дадения интервал от време ще бъде
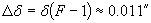
Известно е, че Е 25 се разширява със скорост V = 16.4 km/s. За времето t това образувание ще се е разширило с V.t. Това разширение се вижда от Земята под ъгъл ?? , откъдето намираме разстоянието до мъглявината:
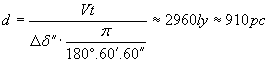
Линейният размер на Е 25 е:
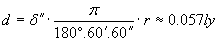
Можем да приемем приблизително, че за времето на живот на образуванието, малката му полуос се е увеличила до този размер със скорост V. Възрастта на образуванието можем да намерим от простото съотношение 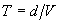 . Но за пресмятанията ще трябва първо да превърнем d в километри, при което ще получим възрастта в секунди. По-лесно е да съобразим, че числената стойност на Т в години време е толкова пъти по-голяма от числената стойност на d в светлинни години, колкото пъти скоростта на светлината ( . Но за пресмятанията ще трябва първо да превърнем d в километри, при което ще получим възрастта в секунди. По-лесно е да съобразим, че числената стойност на Т в години време е толкова пъти по-голяма от числената стойност на d в светлинни години, колкото пъти скоростта на светлината (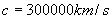 ) е по-голяма от V : ) е по-голяма от V :
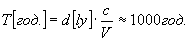
2 задача. Две слънца. Сияйната планета си има не едно, а цели две слънца, същите като нашето Слънце. В тази двойна звездна система планетата се намира в една от точките на Лагранж, която образува равностранен триъгълник с двете звезди. Планетата и двете звезди се движат по кръгови орбити, запазвайки равностранния триъгълник Масата на планетата е много по-малка от масите на звездите – може да се счита, че при движението си звездите не се влияят от нейното присъствие.
• Сияйната планета по размери е същата като Земята. Като цяло тя получава от двете свои слънца също толкова лъчиста енергия в единица време, колкото Земята получава от Слънцето.
• Намерете в астрономически единици дължината на страната на равностранния триъгълник, който планетата образува със звездите. Намерете орбиталния период на системата в земни години.
• Периодът на околоосно въртене на Сияйната планета е 66 земни часа, а нейната ос е перпендикулярна на орбиталната й равнина. Определете продължителността на деня и продължителността на нощта на Сияйната планета. Под ден разбираме времето, през което центровете и на двете слънца са над хоризонта. Не отчитайте рефракцията.
Решение:
Понеже двете звезди са като Слънцето, то масите им считаме за еднакви и равни на масата на Слънцето М0 . Следователно двете звезди се движат около общия си център на масите по окръжност с диаметърd , равен на разстоянието между тях. Дължината на страната на равностранния триъгълник, образуван от Сияйната планета и звездите, е всъщност равна на d . Звездите се движат една около друга под действие само на своите гравитационни сили, а въздействието върху тях на планетата не отчитаме, понеже е нищожно малко. Ето защо, орбиталния период Т на движение на звездите можем да намерим от ІІІ закон на Кеплер в обобщен вид:
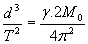
Ако d е в астрономически единици, а Т в години, то можем да напишем:
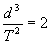
Оттук за орбиталния период получаваме:
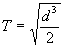 (1) (1)
Светимостите на всяка от звездите също считаме равна на светимостта на Слънцето L0 . Планетата, огрявана от двете звезди, като цяло получава от тях в единица време същата енергия, както Земята от Слънцето. Тъй като размерите на Земята и на Сияйната планета са еднакви, то от тях не зависи общото количество лъчиста енергия, което Земята и планетата получават от своите звезди. За съотношението на разстояниeто d от всяка от звездите до Сияйната планета и разстоянието 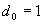 AU от Земята до Слънцето можем да напишем: AU от Земята до Слънцето можем да напишем:
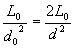
Така получаваме:

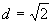 AU ≈ 1.414 AU AU ≈ 1.414 AU
Заместваме в (1), за да получим орбиталния период:
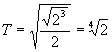 години ≈ 1.189 години години ≈ 1.189 години
Периодът на околоосно въртене на планетата P e свързан с продължителността на слънчевото денонощие P1 чрез следното съотношение:
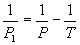
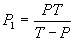
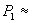 66.42 часа 66.42 часа
Понеже оста на въртене на планетата е перпендикулярна на орбиталната й равнина, продължителностите на деня и на нощтта ще са едни и същи за всички географски ширини, освен на полюсите. За обитател на Сияйната планета всеки ден в небето ще изгряват две слънца, отстоящи на 60° едно след друго. Денят ще започва с изгрева на първото слънце. То ще залезе след период, равен на половината от слънчевото денонощие P1 , след него второто слънце ще остане над хоризонта още в продължение на 1/6 от слънчевото денонощие. Следователно продължителността на деня ще бъде равна на 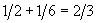 от P1 , или 44.28 часа. Продължителността на нощта ще бъде съответно от P1 , или 44.28 часа. Продължителността на нощта ще бъде съответно 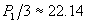 часа. часа.
Тези пресмятания са направени при предположение, че планетата се върти около оста си в същата посока, в която обикаля по орбитата си. Ако планетата се върти обратно, слънчевото денонощие би било 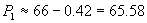 часа. Продължителностите на деня и нощта съответно биха били 43.72 и 21.86 часа. часа. Продължителностите на деня и нощта съответно биха били 43.72 и 21.86 часа.
3 задача. В нощта на 12 юли 2018 г. проф. Никола Каравасилев провежда своите наблюдения на двуметровия телескоп в Националната астрономическа обсерватория Рожен (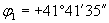 , , 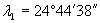 Е). Точно в 22 часа по местно време неговият колега Момчил Петров от Троянската радиоастрофизическа обсерватория регистрира интересно явление и се обажда с молба да се насочи телескопът към обекта за проследяване на явлението във видимата област. Астрономът Петров, както винаги припряно, обяснява на Никола, че това трябва да е звездата Капела, с координати в съответната епоха: Е). Точно в 22 часа по местно време неговият колега Момчил Петров от Троянската радиоастрофизическа обсерватория регистрира интересно явление и се обажда с молба да се насочи телескопът към обекта за проследяване на явлението във видимата област. Астрономът Петров, както винаги припряно, обяснява на Никола, че това трябва да е звездата Капела, с координати в съответната епоха:
α = 5h17m23s, δ = +46°0’23”. След кратко размишление професорът отказва да изпълни молбата.
• Каква е била причината за отказа?
• Щеше ли професорът да се вслуша в молбата, ако се намираше в обсерваторията Туорла, Финландия, с координати: φ2 = +60°24’57”, λ2 = 22°26’36”Е?
Решение:
Нека първо да пресметнем звездното време в момента, в който е постъпила молбата. Датата е 12 юли или 73 дни преди есенното равноденствие. В момента на есенното равноденствие пролетната равноденствена точка отстои на 12h и тогава слънчевото време съвпада със звездното. С всеки изминал ден звездното време избързва напред от слънчевото с 3m56s . Умножавайки 3m56s по 73 получаваме, че на 12 юли звездното време е с 4h47m08s назад спрямо слънчевото. Следователно в момента на наблюдението звездното време e било:
22h – 4h47m08s = 17h12m52s
Капела има ректасцензия α = 5h17m23s . Това означава, че в този момент тя е била около долна кулминация. Бихме могли да се уверим, че звездата се намира под хоризонта, като пресметнем максималната деклинация на незалязващите звезди за географската ширина на Рожен. Тя е:
δ1 = 90° – φ1 = +48°18’25”
Капела се намира южно от тази деклинация и ще е на около 2° под хоризонта. Това е била причината Никола да откаже да насочи телескопа към нея.
За случая в Турку, ако датата и часът по местно време са едни и същи, то и звездното време е същото. Следователно и там Капела ще се намира в долна кулминация. Остава само да оценим дали тя ще е под хоризонта. Обсерваторията Туорла има географска ширина
φ2 = +60°24’57”,
Там максималната деклинация на незалязващите звезди е:
δ1 = 90° – φ2 = +29°35’3”
Капела се намира на около 16,5° северно от този небесен паралел и следователно дори и в долна кулминация ще е над хоризонта и ще може да се наблюдава. Тогава най-вероятно молбата на астронома Петров не би получила отказ.
Нека сега да проверим дали във Финландия Слънцето няма да пречи на наблюденията. Датата е 12 юли, което е около 20 дни след лятното слънцестоене. Това означава, че деклинацията на Слънцето δ0 е близка до максималната 23,5°. В случая ще я примем за 22°. В 22 часа по местно време Слънцето се е намирало почти в долна кулминация. За да намерим височината му h под хоризонта, използваме връзката:
h = δ0 – 90° + φ ≈ 7°
Това означава, че Слънцето няма да е достатъчно ниско под хоризонта, небето ще е светло и наблюденията все пак няма да са възможни.
Ученици старша възраст (до 18 г.)
1 задача. Котешко око. Същата като Задача 1 при младша възраст.
2 задача. Пасаж на Венера. Пресметнете продължителността на централен пасаж на Венера пред диска на Слънцето. По времето, когато от Земята се наблюдава пасажът на Венера, от Венера се наблюдава централна окултация на звезда от Земята. Пресметнете продължителността на тази окултация. Считайте, че Земята и Венера се движат по кръгови орбити, лежащи в една равнина.
Справочни данни:
Радиус на орбитата на Земята – 150 млн. км
Радиус на орбитата на Венера – 108 млн. км
Орбитален период на Венера – 0,615 години
Радиус на Земята – 6378 км
Видим диаметър на слънчевия диск – 32’
Решение:
На схемата е показано разположението на Земята и Венера по време на пасаж. За да се проектира Венера върху слънчевия диск за земния наблюдател, тя трябва да се намира в участъка от орбитата си АВ. От нашата планета Слънцето се вижда под ъгъл 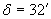 , следователно под такъв ъгъл се вижда и дъгата АВ. Поради факта, че централният ъгъл на тази дъга е малък, ще я апроксимираме с отсечка. , следователно под такъв ъгъл се вижда и дъгата АВ. Поради факта, че централният ъгъл на тази дъга е малък, ще я апроксимираме с отсечка.
Означаваме радиусите на орбитите на Венера и Земята съответно с rV и rT .
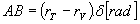
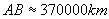
Оттук следва, че ъгълът, под който тази отсечка се вижда от Слънцето (т.е. дъгата, която отсича от орбитата на Венера) е:
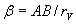
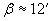
Нека да преминем в отправна система, в която Земята е неподвижна. Това значително улеснява решаването на задачата, защото така не се налага да отчитаме движението на Земята по нейната орбита. Всъщност в тази отправна система Венера се движи с по-малка ъглова скорост, отколкото в действителност:
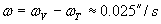
където 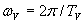 и и 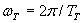 са ъгловите скорости на Венера и Земята (С TV и TT сме означили орбиталните периоди на двете плранети). са ъгловите скорости на Венера и Земята (С TV и TT сме означили орбиталните периоди на двете плранети).
За да пресече областта АВ (т.е. за да премине пред диска на Слънцето за земния наблюдател), Венера трябва да измине ъгъл β по своята орбита. В избраната отправна система тя се движи с ъглова скорост ω и това ще стане за интервал от време:
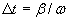
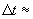 8 часа 8 часа
Следователно един централен пасаж на Венера пред диска на Слънцето ще продължи около 8 часа.
За да отговорим на втория въпрос, нека първо да намерим скоростите на движение на двете планети VV и VT . Те са:
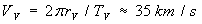
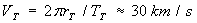
В момента на пасажа двете планети се движат успоредно една на друга. Следователно, относителната им скорост на движение е:
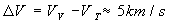
Гледано от Венера, за времето на окултацията Земята се премества на един свой диаметър (тъй като считаме звездите за точкови обекти). Означаваме с RT радиуса на Земята и намираме търсената продължителност:

3 задача. Апекс на Слънчевата система (адаптирана от Б. А. Воронцов-Вельяминов, Сборник задач и практических упражнений по астрономии) . В преследване на все по-трудни задачи и научни приключения, младите астрономи Момчил Молнар и Тошко Димитров са решили да тръгнат към апекса на Слънчевата система. Двамата търпеливо са пресметнали средните лъчеви скорости на звезди, които се съдържат в 6 квадрата от небесната сфера, всеки със страна 40°, намиращи се в различни направления.
Като използвате тази информация, определете координатите на апекса на Слънчевата система и нейната скорост на движение спрямо наблюдаваните звезди.
Как мислите, какво ще стане, когато Момчил и Тодор стигнат до апекса?
Решение:
Скоростта на Слънцето относно звездите можем да представим като вектор, чиито компоненти, насочени по три взаимно перпендикулярни оси, можем да пресметнем по дадените ни данни. Нека две от осите лежат в равнината на небесния екватор. Приемаме, че оста Х е насочена към пролетната равноденствена точка и компонентата на нашата скорост Vx по нея намираме от данните за І и ІІ квадрат. Положителната стойност на лъчевите скорости на звездите означава, че ние се отдалечаваме с такава скорост в посока от тях, а отрицателната стойност – че се движим в посока към звездите. По принцип би трябвало лъчевата скорост на звездите, пресметната за квадрат І да е равна по големина и обратна по знак на скоростта за квадрат ІІ. Но това не е така, защото става въпрос за статистически пресмятания, основани на много звезди, които на свой ред извършват различни движения. Ето защо, за по-голяма точност приемаме, че компонентата на нашата скорост по оста X e:
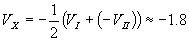 км/с км/с
където VI и VII са средните лъчеви скорости на звездите в І и ІІ квадрат.
По аналогичен начин получаваме:
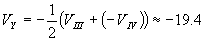 км/с км/с
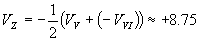 км/с км/с
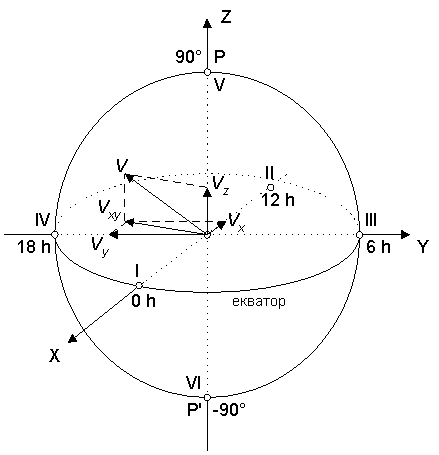
На чертежа е означена пълната скорост V на Слънчевата система относно звездите и нейните компоненти по трите оси.
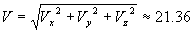 км/с км/с
За да намерим координатите на апекса на Слънчевата система, първо събираме векторно компонетите Vx и Vy и получаваме скоростта в равнината на небесния екватор Vxy . Деклинацията δ на апекса е ъгълът между V и Vxy :
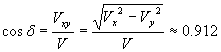

Ректасцензията на апекса е ъгълът между оста Х и Vxy . Първо намираме ъгъла между Vx и Vxy :
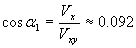
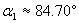
Ректасцензията на апекса е:
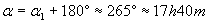
Тази точка се намира на границата между съзвездията Херкулес и Лира.
Въпросът какво ще стане, когато стигнем до апекса не е по-смислен, отколкото какво ще стане, когато стигнем до хоризонта или до северния небесен полюс, например. Това е въпрос-шега, но за по-големи подробности все пак трябва да попитаме космическите пътешественици Момчил и Тодор.
|