Задача:

Оценете приблизително каква част от повърхността на Луната се огрява от Слънцето в даден момент. А от повърхността на Земята?

Решение:

Приближен отговор на първия въпрос е, че Слънцето огряба половината от Луната. Но ако искаме да бъдем по-точни, трябва да отчетем факта, че Слънцето е по-голямо от Луната. На чертежа се вижда, че поради това то огрява наведнъж малко повече от половината Луна. Можем да пресметнем приблизително колко повече.

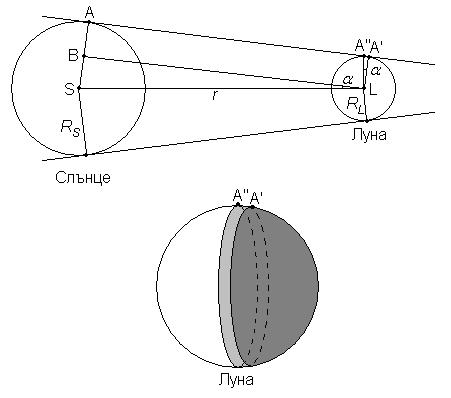
Лъчът AA' е допирателен към повърхностите на Слънцето и Луната и точка A' лежи на една окръжност, която бележи границата на огряната от Слънцето страна на Луната. Точката A" лежи на окръжност, която разполовява Луната точно на две равни части и е перпендикулярна на правата Луна-Слънце. Да пресметнем площта на ивицата от лунната повърхност между тези две окръжности. На горния чертеж отсечката LB е перпендикулярна на SA. Ъглите SLB и A'LA" са равни, тъй като са с взаимно перпендикулярни рамене:

<SLB = <A'LA" = α

От триъгълник SLB определяме:

sin α = (R_S - R_L)/r

където R_S и R_L са радиусите на Слънцето и Луната, а r е разстоянието между тях. Понеже R_S >> R_L, то можем да напишем:

sin α ≈ R_S/r ≈ 700 000 km /150 000 000 km ≈0.0047

α ≈ 0.267° ≈16'

За площта на ивицата получаваме приблизително:

ΔS ≈ 2πR_L × A'A" = 2πR_L × R_Lα[rad] = 2πR_L × R_L.R_S/r

ΔS ≈ 2πR_L² ×0.00467

Можем да представим това по следния начин:

ΔS = 4πR_L² ×0.0023 = 0.0023.S_L

където S_L= 4πR_L² е площта на цялата повръхност на Луната.

Оттук следва, че Слънцето огрява половината от повърхността на Луната плюс още около 0.23% от цялата лунна повърхност, или общо 50.23%.

Тъй като и земният радиус е много по-малък от слънчевия, можем да получим по аналогичен начин същия резултата и за Земята. Такъв отговор, обаче, би бил верен, само ако Земята нямаше атмосфера. Поради наличието на атмосфера, трябва да отчетем и рефракцията. На хоризонта ъгълът на рефракция е около половин градус, следователно той е около два пъти по-голям от ъгъла α. Това означава, че допълнителната ивица от земната повърхност, над половината, ще съответства на ъгъл:

α + 2α = 3α

Тъй като отново става въпрос за малък ъгъл, можем приблизително да пресметнем, че частта от земната повърхност, огрявана от Слънцето, ще бъде:

50.23% + 2 × 0.23% = 50.69%